5. Optimización y visualización

“Entre la teoría y la práctica, hay una diferencia más grande que la diferencia entre la teoría y la práctica.” - Yann LeCun, ganador del Premio Turing en 2018

El éxito de los modelos de deep learning depende en gran medida de algoritmos de optimización eficaces y estrategias adecuadas de inicialización de pesos. En este capítulo, exploramos a fondo los métodos de optimización e inicialización que son elementos clave en el aprendizaje de modelos de deep learning, y presentamos formas de entender intuitivamente estos procesos a través de la visualización. Primero, examinamos el desarrollo y los principios matemáticos de diversos métodos de inicialización de pesos, que son fundamentales para el aprendizaje de redes neuronales. Luego, analizamos y comparamos las características y rendimiento de algoritmos de optimización modernos, comenzando con el descenso del gradiente (Gradient Descent), y pasando por Adam, Lion, Sophia, AdaFactor, entre otros. En particular, no solo exploramos los fundamentos teóricos, sino también cómo cada algoritmo funciona en la práctica durante el proceso de aprendizaje de modelos de deep learning a través de experimentación. Finalmente, presentamos diversas técnicas para visualizar y analizar espacios de funciones de pérdida (loss landscape) de alta dimensión, proporcionando una comprensión profunda de las dinámicas de aprendizaje de los modelos de deep learning.

5.1 Evolución y enfoque moderno en la inicialización de parámetros

La inicialización de parámetros en redes neuronales es un elemento clave que determina la convergencia, la eficiencia del aprendizaje y el rendimiento final del modelo. Una inicialización incorrecta puede ser una causa principal de fallos en el aprendizaje. PyTorch proporciona diversos métodos de inicialización a través del módulo torch.nn.init, y se pueden encontrar detalles adicionales en la documentación oficial. La evolución de los métodos de inicialización refleja el esfuerzo de los investigadores de deep learning para superar las dificultades del aprendizaje en redes neuronales. En particular, una inicialización inadecuada puede causar problemas como la desaparición (vanishing gradient) o explosión (exploding gradient) del gradiente, que son obstáculos principales para el aprendizaje en redes neuronales profundas. Con la aparición de modelos de lenguaje a gran escala (Large Language Models, LLMs) como GPT-3 y LaMDA, la importancia de la inicialización se ha destacado aún más. A medida que aumenta el tamaño del modelo, la distribución de los parámetros iniciales tiene un impacto cada vez mayor en las primeras etapas del aprendizaje. Por lo tanto, seleccionar una estrategia de inicialización adecuada según las características y el tamaño del modelo se ha convertido en una etapa esencial en el desarrollo de modelos de deep learning.

5.1.1 Principios matemáticos de los métodos de inicialización

El desarrollo de los métodos de inicialización de redes neuronales es resultado de un profundo trabajo teórico y numerosas validaciones experimentales. Cada método de inicialización ha sido diseñado para abordar situaciones específicas (por ejemplo, el uso de funciones de activación particulares, la profundidad de la red, el tipo de modelo) o para mejorar las dinámicas de aprendizaje, evolucionando con el tiempo para enfrentar nuevos desafíos.

A continuación se presentan los métodos de inicialización que serán analizados y comparados en detalle en este libro. (El código completo de implementación está incluido en el archivo chapter_04/initialization/base.py.)

!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your local

%load_ext autoreload
%autoreload 2

import torch
import torch.nn as nn
import numpy as np

# Set seed
np.random.seed(7)
torch.manual_seed(7)


from dldna.chapter_05.initialization.base import init_methods, init_weights_lecun, init_weights_scaled_orthogonal, init_weights_lmomentum # init_weights_emergence, init_weights_dynamic 삭제

init_methods = {
    # Historical/Educational Significance
    'lecun': init_weights_lecun,        # The first systematic initialization proposed in 1998
    'xavier_normal': nn.init.xavier_normal_, # Key to the revival of deep learning in 2010
    'kaiming_normal': nn.init.kaiming_normal_, # Standard for the ReLU era, 2015

    # Modern Standard
    'orthogonal': nn.init.orthogonal_,  # Important in RNN/LSTM
    'scaled_orthogonal': init_weights_scaled_orthogonal, # Optimization of deep neural networks

    # 2024 Latest Research
    'l-momentum': init_weights_lmomentum # L-Momentum Initialization
}

Inicialización Tradicional

• Inicialización de LeCun (1998): \(std = \sqrt{\frac{1}{n_{in}}}\)

  • Método propuesto por Yann LeCun en 1998, que determina la desviación estándar de los pesos considerando solo la dimensión de entrada (\(n_{in}\)). Se diseñó para evitar que las salidas de cada neurona varíen significativamente con el número de entradas. Sin embargo, en redes profundas, tendía a reducir la varianza de los valores de activación a medida que se profundizaba en las capas. Este problema era particularmente notable cuando se utilizaban funciones de activación sigmoidales como tanh.

Inicialización Moderna

• Inicialización Xavier (Glorot, 2010): \(std = \sqrt{\frac{2}{n_{in} + n_{out}}}\)

  • Método propuesto por Xavier Glorot y Yoshua Bengio que considera tanto la dimensión de entrada (\(n_{in}\)) como la de salida (\(n_{out}\)) para mitigar el problema del desvanecimiento/explotación de gradientes. El objetivo es mantener adecuadamente la varianza de los valores de activación y los gradientes en cada capa. Es particularmente efectivo cuando se utiliza con funciones de activación saturadas como sigmoid, tanh.

• Inicialización Kaiming (He, 2015): \(std = \sqrt{\frac{2}{n_{in}}}\)

  • Método propuesto por Kaiming He y otros que considera las características de la función de activación ReLU (que convierte los valores negativos en cero). Dado que ReLU tiende a reducir la varianza de los valores de activación a la mitad, se utiliza una varianza mayor (\(\sqrt{2}\) veces) que la inicialización Xavier para compensar esto. Esto reduce el problema de “neuronas muertas” y permite un aprendizaje estable en redes profundas, convirtiéndose en un estándar de facto cuando se utilizan funciones de activación tipo ReLU.

Últimas Inicializaciones (después de 2023)

• Inicialización L-Momentum (Zhuang, 2024)

  • La inicialización L-Momentum es un método propuesto en 2024 que controla el L-momentum de las matrices de pesos iniciales, inspirado en los algoritmos de optimización basados en momentum.

  • Fórmula:

    \(W \sim U(-\sqrt{\frac{6}{n_{in}}}, \sqrt{\frac{6}{n_{in}}})\) \(W = W \cdot \sqrt{\frac{\alpha}{Var(W)}}\)

    Donde \(U\) es una distribución uniforme, y \(\alpha\) es un valor que representa el L-momentum, utilizando el cuadrado del momentum del optimizador.

  • El objetivo es reducir la variabilidad de los gradientes en las etapas iniciales para proporcionar una ruta de aprendizaje más estable.

  • Es aplicable a diversos optimizadores y funciones de activación, y ha demostrado contribuir a tasas de aprendizaje más altas, convergencia rápida y mejor desempeño general.

Principios Matemáticos

La mayoría de los métodos de inicialización moderna siguen (explícita o implícitamente) los siguientes tres principios fundamentales.

1. Preservación de Varianza (Variance Preservation): La varianza de los valores de activación durante la propagación hacia adelante y la varianza de los gradientes durante la propagación hacia atrás deben mantenerse constantes en cada capa.

   \(Var(y) \approx Var(x)\)

   Esto ayuda a evitar que las señales se vuelvan demasiado grandes o pequeñas, facilitando un aprendizaje más estable.

2. Control Espectral (Spectral Control): Se debe controlar la distribución de los valores singulares de la matriz de pesos para garantizar la estabilidad numérica durante el proceso de aprendizaje.

   \(\sigma_{max}(W) / \sigma_{min}(W) \leq C\)

   Esto es particularmente importante en estructuras como las redes neuronales recurrentes (RNN), donde la matriz de pesos se multiplica repetidamente.

3. Optimización de la expresividad (Expressivity Optimization): se debe maximizar el rango efectivo de las matrices de pesos para que la red tenga una suficiente capacidad de expresión.

   \(rank_{eff}(W) = \frac{\sum_i \sigma_i}{\max_i \sigma_i}\) Las investigaciones recientes han estado esforzándose por satisfacer explícitamente estos principios.

En conclusión, el método de inicialización debe seleccionarse cuidadosamente teniendo en cuenta la interacción con el tamaño del modelo, su estructura, las funciones de activación y los algoritmos de optimización. Esto se debe a que tiene un gran impacto en la velocidad de aprendizaje, la estabilidad y el rendimiento final del modelo.

Haga clic para ver el contenido (deep dive: principios matemáticos y técnicas avanzadas de la inicialización de redes neuronales profundas)

Principios matemáticos y técnicas avanzadas de inicialización de redes neuronales profundas

1. Principio de preservación de la varianza (Variance Preservation Principle)

1.1 Fundamento teórico

A medida que aumenta la profundidad de la red neuronal, es muy importante preservar las características estadísticas del señal (especialmente la varianza) durante el proceso de propagación hacia adelante (forward propagation) y el proceso de retropropagación (backpropagation). Esto evita que la señal se desvanezca (vanishing) o explote (exploding), lo cual permite un aprendizaje estable.

Denotemos los valores de activación del \(l\)-ésimo nivel como \(h_l\), la matriz de pesos como \(W_l\), el sesgo como \(b_l\), y la función de activación como \(f\). La propagación hacia adelante se expresa de la siguiente manera:

\(h_l = f(W_l h_{l-1} + b_l)\)

Si asumimos que los elementos del señal de entrada \(h_{l-1} \in \mathbb{R}^{n_{in}}\) son variables aleatorias independientes con media 0 y varianza \(\sigma^2_{h_{l-1}}\), y que los elementos de la matriz de pesos \(W_l \in \mathbb{R}^{n_{out} \times n_{in}}\) son variables aleatorias independientes con media 0 y varianza \(Var(W_l)\), y el sesgo \(b_l = 0\), entonces, asumiendo que la función de activación es lineal, se tiene:

\(Var(h_l) = n_{in} Var(W_l) Var(h_{l-1})\) (donde \(n_{in}\) es la dimensión de entrada del \(l\)-ésimo nivel)

Para preservar la varianza de los valores de activación, debe cumplirse que \(Var(h_l) = Var(h_{l-1})\), por lo tanto, se necesita que \(Var(W_l) = 1/n_{in}\).

Durante la retropropagación, para el error \(\delta_l = \frac{\partial L}{\partial h_l}\) (donde \(L\) es la función de pérdida), se cumple la siguiente relación:

\(\delta_{l-1} = W_l^T \delta_l\) (asumiendo que la función de activación es lineal)

Por lo tanto, para preservar la varianza durante la retropropagación, debe cumplirse que \(Var(\delta_{l-1}) = n_{out}Var(W_l)Var(\delta_l)\), por lo tanto, se necesita que \(Var(W_l) = 1/n_{out}\) (donde \(n_{out}\) es la dimensión de salida del \(l\)-ésimo nivel).

1.2 Extensión a funciones de activación no lineales

Función de activación ReLU

La función ReLU (\(f(x) = max(0, x)\)) tiende a reducir la varianza de los valores de activación porque anula la mitad de las entradas. Kaiming He propuso corregir esto utilizando la siguiente fórmula de preservación de la varianza:

\(Var(W_l) = \frac{2}{n_{in}} \quad (\text{especial para ReLU})\)

Esta fórmula compensa la reducción de varianza causada por el paso a través de ReLU, aumentándola en un factor de 2.

Función de activación Leaky ReLU

Para la función Leaky ReLU (\(f(x) = max(\alpha x, x)\), donde \(\alpha\) es una constante pequeña), la fórmula generalizada es:

\(Var(W_l) = \frac{2}{(1 + \alpha^2) n_{in}}\)

1.3 Enfoque probabilístico (referencia)

También se puede utilizar el inverso de la matriz de información de Fisher (FIM) para inicializar los pesos. La FIM contiene información sobre la curvatura del espacio de parámetros, lo cual permite una inicialización más eficiente. (Para más detalles, ver [4] Martens, 2020).

2. Control espectral (Spectral Control)

2.1 Descomposición en valores singulares y dinámica del aprendizaje

La descomposición en valores singulares (Singular Value Decomposition, SVD) de la matriz de pesos \(W \in \mathbb{R}^{m \times n}\) se expresa como \(W = U\Sigma V^T\). Aquí, \(\Sigma\) es una matriz diagonal, cuyos elementos diagonales son los valores singulares de \(W\) (\(\sigma_1 \geq \sigma_2 \geq ... \geq 0\)). Si el valor singular máximo de la matriz de pesos (\(\sigma_{max}\)) es demasiado grande, puede causar un gradiente explosivo (exploding gradient), y si el valor singular mínimo (\(\sigma_{min}\)) es demasiado pequeño, puede causar un gradiente desvanecido (vanishing gradient).

Por lo tanto, es importante controlar la proporción de los valores singulares (número de condición, condition number) \(\kappa = \sigma_{max}/\sigma_{min}\). Cuanto más cercano a 1 sea \(\kappa\), mayor será la estabilidad del flujo de gradientes.

Teorema 2.1 (Saxe et al., 2014): En una red neuronal lineal profunda inicializada ortogonalmente, si cada matriz de pesos \(W_l\) es una matriz ortogonal, la norma Frobenius de la matriz jacobiana \(J\) del output con respecto a la entrada se mantiene en 1.

\(||J||_F = 1\)

Esto ayuda a mitigar los problemas de gradiente desvanecido o explosivo incluso en redes muy profundas.

2.2 Normalización espectral dinámica

Miyato et al. (2018) propusieron la técnica de Normalización Espectral para mejorar la estabilidad del entrenamiento de GANs, limitando la norma espectral (valor singular máximo) de las matrices de pesos.

\(W_{SN} = \frac{W}{\sigma_{max}(W)}\)

Este método ha demostrado ser particularmente efectivo en el entrenamiento de GANs y recientemente se ha aplicado a otros modelos, como Vision Transformers.

3. Optimización de la expresividad

3.1 Teoría del rango efectivo

La capacidad de una matriz de pesos \(W\) para representar diversas características (features) puede medirse por la uniformidad de la distribución de los valores singulares. El rango efectivo se define como:

\(\text{rank}_{eff}(W) = \exp\left( -\sum_{i=1}^r p_i \ln p_i \right) \quad \text{donde } p_i = \frac{\sigma_i}{\sum_j \sigma_j}\)

Aquí, \(r\) es el rango de \(W\), \(\sigma_i\) es el \(i\)-ésimo valor singular y \(p_i\) es el valor singular normalizado. El rango efectivo es una métrica que indica la distribución de los valores singulares; cuanto mayor sea su valor, más uniformemente distribuidos estarán los valores singulares, lo cual implica una mayor expresividad.

3.2 Tabla de comparación de estrategias de inicialización

Estrategia	Descripción
Inicialización aleatoria	Los pesos se inicializan con valores aleatorios.
Inicialización Xavier/Glorot	Los pesos se inicializan con una distribución normal o uniforme, ajustando la varianza para mantener el flujo de gradientes estable.
Inicialización He	Similar a Xavier, pero optimizada para funciones de activación ReLU.
Inicialización ortogonal	Los pesos se inicializan como matrices ortogonales para mantener la norma Frobenius del Jacobiano en 1.
Método de inicialización	Distribución de valores singulares
————————	————————————————————————————————–
Xavier	Disminuye relativamente rápidamente
Kaiming	Ajustado para la función de activación ReLU (disminuye menos)
Ortogonal	Todos los valores singulares son 1
Promoviendo Emergencia	Se ajusta según el tamaño de la red, disminuye relativamente lentamente (cercano a una distribución heavy-tailed)

3.3 Inicialización Promoviendo Emergencia

La inicialización Promoviendo Emergencia es una técnica reciente propuesta para fomentar habilidades emergentes en modelos de lenguaje a gran escala (LLM). Este método ajusta la varianza de los pesos iniciales según el tamaño de la red (específicamente, la profundidad de las capas), lo que tiene el efecto de aumentar el rango efectivo.

Chen et al. (2023) propusieron un factor de escala \(\nu_l\) en modelos Transformer como sigue:

\(\nu_l = \frac{1}{\sqrt{d_{in}}} \left( 1 + \frac{\ln l}{\ln d} \right)\)

Donde \(d_{in}\) es la dimensión de entrada, \(l\) es el índice de la capa, y \(d\) es la profundidad del modelo. Este factor de escala se multiplica por la desviación estándar de las matrices de pesos para la inicialización. Es decir, se muestrean desde una distribución normal con \(\nu_l \sqrt{2/n_{in}}\) como desviación estándar.

4. Interacción entre inicialización y optimización

4.1 Extensión de la teoría NTK

La teoría del Kernel Tangente Neuronal (NTK) de Jacot et al. (2018) es una herramienta útil para analizar la dinámica de aprendizaje en redes neuronales “muy anchas” (infinitely wide). Según la teoría NTK, se espera que la matriz hessiana de una red muy ancha sea proporcional a la identidad en el punto de inicialización. Es decir,

\(\lim_{n_{in} \to \infty} \mathbb{E}[\nabla^2 \mathcal{L}] \propto I\) (en el punto de inicialización)

Esto sugiere que la inicialización Xavier proporciona una inicialización cercana a lo óptimo en redes muy anchas.

4.2 Estrategias de inicialización meta

Investigaciones recientes, como MetaInit (2023), proponen métodos para aprender la distribución de inicialización óptima para una arquitectura y conjunto de datos dados a través del aprendizaje meta.

\(\theta_{init} = \arg\min_\theta \mathbb{E}_{\mathcal{T}}[\mathcal{L}(\phi_{fine-tune}(\theta, \mathcal{T}))]\)

Donde \(\theta\) son los parámetros de inicialización, \(\mathcal{T}\) es la tarea de entrenamiento, y \(\phi\) representa el proceso de fine-tuning de un modelo inicializado con \(\theta\).

5. (Referencia) Técnicas de inicialización basadas en física

Recientemente, también se están investigando métodos de inicialización inspirados en los principios de la física. Por ejemplo, se han propuesto métodos que imitan la ecuación de Schrödinger de la mecánica cuántica o las ecuaciones de Navier-Stokes de la dinámica de fluidos para optimizar el flujo de información entre capas. Sin embargo, estos métodos aún están en una etapa inicial de investigación y su utilidad práctica no ha sido verificada.

6. Recomendaciones Prácticas

1. Arquitectura CNN: Generalmente es recomendable usar la inicialización Kaiming (He initialization) junto con la normalización por lotes (Batch Normalization).
2. Transformadores: Se utilizan ampliamente la Inicialización Ortogonal Escalada (ajuste de valores singulares) o la inicialización Xavier.
3. Modelos de Lenguaje Grandes (LLM): Deben considerarse métodos de inicialización especializados para modelos grandes, como la inicialización que promueve el surgimiento (Emergence-Promoting Initialization).
4. Neural ODE: Se utilizan los métodos habituales a menos que haya una situación especial.

---

Referencias

1. He et al. “Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification”, ICCV 2015
2. Saxe et al. “Exact solutions to the nonlinear dynamics of learning in deep linear neural networks”, ICLR 2014
3. Jacot et al. “Neural Tangent Kernel: Convergence and Generalization in Neural Networks”, NeurIPS 2018
4. Martens, J. “New insights and perspectives on the natural gradient method.” The Journal of Machine Learning Research, 2020.
5. Chen et al. “Towards Understanding Large Language Models: A Transformative Reading List”, arXiv preprint arXiv:2307.12980, 2023. (Relacionado con la inicialización que promueve el surgimiento)
6. Miyato et al., “Spectral Normalization for Generative Adversarial Networks”, ICLR 2018

5.1.2 Métodos de inicialización: análisis comparativo práctico

Para comprender cómo los diferentes métodos de inicialización vistos anteriormente afectan realmente el aprendizaje del modelo, realizaremos experimentos de comparación utilizando un modelo simple. Entrenaremos modelos con cada método de inicialización bajo las mismas condiciones y analizaremos los resultados. Los criterios de evaluación son los siguientes.

Criterio de Evaluación	Significado	Características Deseables
Tasa de Error (%)	Rendimiento predictivo del modelo final (mejor si es bajo)	Mejor si es bajo
Velocidad de Convergencia	Pendiente de la curva de aprendizaje (indicador de estabilidad de aprendizaje)	Baja (más empinada) converge más rápido
Número de Condición Promedio	Estabilidad numérica de las matrices de pesos	Mejor si es bajo (cercano a 1)
Norma Espectral	Tamaño de la matriz de pesos (mayor valor singular)	Se necesita un valor adecuado, no demasiado grande ni pequeño
Razón de Rango Efectivo	Expresividad de la matriz de pesos (uniformidad en la distribución de valores singulares)	Mejor si es alta
Tiempo de Ejecución(s)	Tiempo de aprendizaje	Mejor si es bajo

from dldna.chapter_04.models.base import SimpleNetwork
from dldna.chapter_04.utils.data import get_data_loaders, get_device
from dldna.chapter_05.initialization.base import init_methods
from dldna.chapter_05.initialization.analysis import analyze_initialization, create_detailed_analysis_table
import torch.nn as nn

device = get_device()
# Initialize data loaders
train_dataloader, test_dataloader = get_data_loaders()

# Detailed analysis of initialization methods
results = analyze_initialization(
    model_class=lambda: SimpleNetwork(act_func=nn.PReLU()),
    init_methods=init_methods,
    train_loader=train_dataloader,
    test_loader=test_dataloader,
    epochs=3,
    device=device
)

# Print detailed analysis results table
create_detailed_analysis_table(results)

Initialization method: lecun

/home/sean/Developments/expert_ai/books/dld/dld/chapter_04/experiments/model_training.py:320: UserWarning: std(): degrees of freedom is <= 0. Correction should be strictly less than the reduction factor (input numel divided by output numel). (Triggered internally at ../aten/src/ATen/native/ReduceOps.cpp:1823.)
  'std': param.data.std().item(),

Initialization method: xavier_normal

Initialization method: kaiming_normal

Initialization method: orthogonal

Initialization method: scaled_orthogonal

Initialization method: l-momentum

Initialization Method | Error Rate (%) | Convergence Speed | Average Condition Number | Spectral Norm | Effective Rank Ratio | Execution Time (s)
---------------------|--------------|-----------------|------------------------|-------------|--------------------|------------------
lecun        | 0.48 | 0.33 | 5.86 | 1.42 | 0.89 | 30.5
xavier_normal | 0.49 | 0.33 | 5.53 | 1.62 | 0.89 | 30.2
kaiming_normal | 0.45 | 0.33 | 5.85 | 1.96 | 0.89 | 30.1
orthogonal   | 0.49 | 0.33 | 1.00 | 0.88 | 0.95 | 30.0
scaled_orthogonal | 2.30 | 1.00 | 1.00 | 0.13 | 0.95 | 30.0
l-momentum   | nan | 0.00 | 5.48 | 19.02 | 0.89 | 30.1

Los resultados del experimento se resumen en la siguiente tabla.

Método de Inicialización	Tasa de Error (%)	Velocidad de Convergencia	Número de Condición Promedio	Norma Espectral	Proporción de Rango Efectivo	Tiempo de Ejecución (s)
lecun	0.48	0.33	5.66	1.39	0.89	23.3
xavier_normal	0.48	0.33	5.60	1.64	0.89	23.2
kaiming_normal	0.45	0.33	5.52	1.98	0.89	23.2
orthogonal	0.49	0.33	1.00	0.88	0.95	23.3
scaled_orthogonal	2.30	1.00	1.00	0.13	0.95	23.3
l-momentum	nan	0.00	5.78	20.30	0.89	23.2

Los puntos destacados de los resultados del experimento son los siguientes.

1. Excelente rendimiento de la inicialización Kaiming: La inicialización Kaiming mostró la tasa de error más baja, con un 0.45%. Este resultado demuestra una combinación óptima con las funciones de activación ReLU, lo que confirma nuevamente la eficacia de la inicialización Kaiming cuando se usa con funciones del tipo ReLU.

2. Estabilidad de los métodos ortogonales: La inicialización ortogonal mostró el número de condición más bajo (1.00), lo que indica una excelente estabilidad numérica. Esto significa que durante el proceso de aprendizaje, los gradientes no se distorsionan y se propagan correctamente, lo cual es particularmente importante en modelos como las redes neuronales recurrentes (RNN), donde las matrices de pesos se multiplican repetidamente. Sin embargo, en este experimento la tasa de error fue relativamente alta, lo que podría deberse a las características del modelo utilizado (una MLP simple).

3. Problemas con la inicialización ortogonal escalada: La inicialización ortogonal escalada mostró una tasa de error muy alta, del 2.30%. Esto sugiere que este método de inicialización no es adecuado para el modelo y conjunto de datos utilizados, o que se requieren ajustes adicionales de hiperparámetros. Es posible que el factor de escala (scaling factor) sea demasiado pequeño, lo que impide un aprendizaje adecuado.

4. Inestabilidad de la inicialización de L-Momentum: L-Momentum tiene una tasa de error y velocidad de convergencia de nan y 0.00, lo que indica que no se realizó ningún aprendizaje. El espectro norma de 20.30 es muy alto, lo que sugiere que los valores iniciales de los pesos podrían ser demasiado grandes, causando divergencia.

5.1.3 Recomendaciones prácticas y consideraciones adicionales

La inicialización de modelos de deep learning es un hiperparámetro que debe seleccionarse cuidadosamente teniendo en cuenta la arquitectura del modelo, las funciones de activación, los algoritmos de optimización y las características del conjunto de datos. A continuación se presentan aspectos a considerar al elegir métodos de inicialización en la práctica.

Principios básicos

• Funciones de activación ReLU:
  • Inicialización Kaiming (He initialization): Este es el método de inicialización más utilizado actualmente con ReLU y sus variantes (Leaky ReLU, ELU, SELU, etc.). Está bien respaldado tanto por resultados experimentales como por fundamentos teóricos (preservación de la varianza).
  • L-Momentum Initialization: Si se utilizan optimizadores basados en Momentum, como Adam o AdamW, esto puede ser una opción a considerar.
• Funciones de activación Sigmoid, Tanh:
  • Inicialización Xavier (Glorot initialization): Estas funciones de activación pueden sufrir el problema del desvanecimiento del gradiente (vanishing gradient problem) si los valores de entrada son muy grandes o muy pequeños. Por lo tanto, la inicialización Xavier sigue siendo una opción válida.
• Redes neuronales recurrentes (RNN, LSTM, GRU):
  • Inicialización Ortogonal: En modelos RNN con conexiones recurrentes, es importante mantener los valores singulares de las matrices de pesos cerca de 1. La inicialización ortogonal asegura esto y ayuda a mitigar problemas de explosión/degeneración del gradiente y facilita el aprendizaje de dependencias a largo plazo (long-range dependency).
  • Nota: La inicialización ortogonal se aplica típicamente a la matriz de pesos hidden-to-hidden en RNN, mientras que para la matriz de pesos input-to-hidden se suele usar otro método de inicialización (por ejemplo, Kaiming).

Escala y características del modelo

• Redes neuronales profundas generales (menos de 50 capas):
  • En muchos casos, la inicialización Kaiming (para funciones ReLU) o Xavier (para Sigmoid/Tanh) es suficiente.
• Redes neuronales muy profundas (más de 50 capas):
  • Conexiones residuales (ResNet): Si el modelo tiene conexiones residuales, la inicialización Kaiming funciona bien.
  • Sin conexiones residuales (ResNet): Se debe ser más cauteloso con la inicialización. Considerar métodos como Scaled Orthogonal o Fixup Initialization.
• Modelos de gran escala (1B+ parámetros):
  • L-Momentum Initialization
  • Inicialización a cero (en partes específicas): Inicializar a 0 ciertas partes del modelo, como la proyección de salida de capas de atención en modelos Transformer, puede ser efectivo. (Referencia: Megatron-LM)
  • Nota: Los modelos de gran escala tienden a ser inestables durante el entrenamiento, por lo que además de la inicialización, es importante combinar cuidadosamente otras técnicas como programación del tasa de aprendizaje, recorte de gradiente y métodos de regularización.

Consideraciones adicionales

• Normalización por lotes (Batch Normalization) / Normalización de capa (Layer Normalization): las técnicas de normalización reducen algo la importancia de la inicialización, pero no la reemplazan completamente. Aún es recomendable elegir una inicialización adecuada.
• Aprendizaje por transferencia (Transfer Learning): cuando se utilizan modelos preentrenados, es común mantener los pesos preentrenados o aplicar la inicialización de Kaiming/Xavier con tasas de aprendizaje pequeñas solo a las capas que se afinarán.
• Algoritmos de optimización: dependiendo del optimizador utilizado, puede haber una inicialización más adecuada. Por ejemplo, si se utiliza el optimizador Adam, se puede aplicar la inicialización L-Momentum.
• Experimentación y validación: el mejor método de inicialización puede variar según el problema y los datos. Es importante probar varios métodos de inicialización y seleccionar el que ofrece el mejor rendimiento en el conjunto de validación.

La inicialización es como el “héroe oculto” del aprendizaje profundo. Una inicialización adecuada puede determinar el éxito o fracaso del entrenamiento del modelo, maximizando su rendimiento y reduciendo significativamente el tiempo de entrenamiento. Basándose en las pautas presentadas en esta sección y las tendencias actuales de la investigación, esperamos que puedan encontrar la estrategia de inicialización más adecuada para sus modelos de aprendizaje profundo.

5.2 Algoritmos de optimización: el motor central del aprendizaje profundo

Desafío: ¿Cómo se pueden resolver los problemas de caer en mínimos locales (local minima) o que la velocidad de aprendizaje sea demasiado lenta con el descenso del gradiente (Gradient Descent)?

Lamentación del investigador: Reducir simplemente la tasa de aprendizaje no fue suficiente. En algunos casos, el aprendizaje se volvió demasiado lento y tomaba mucho tiempo, mientras que en otros casos divergía y fallaba. Al igual que tanteando un camino montañoso envuelto en niebla, encontrar el óptimo ha sido una tarea ardua. Aparecieron diversos algoritmos de optimización como momentum, RMSProp y Adam, pero aún no existe una solución universal perfecta para todos los problemas.

El impresionante desarrollo del aprendizaje profundo no solo se debe a la innovación en la estructura del modelo, sino también al avance de los algoritmos de optimización eficientes. Los algoritmos de optimización son como el motor central que automatiza y acelera el proceso de encontrar el mínimo de la función de pérdida. La eficiencia y estabilidad de este motor determinan la velocidad de aprendizaje y el rendimiento final del modelo de aprendizaje profundo.

5.2.1 Evolución e implementación de algoritmos de optimización - una evolución continua

Los algoritmos de optimización han evolucionado durante las últimas décadas, al igual que los seres vivos, resolviendo tres tareas centrales.

1. Eficiencia computacional (Computational Efficiency): Se debe completar el aprendizaje lo más rápido posible con recursos de cómputo limitados.
2. Rendimiento de generalización (Generalization Performance): Debe ofrecer un buen rendimiento no solo en los datos de entrenamiento, sino también en nuevos datos.
3. Escala (Scalability): Debe funcionar de manera estable incluso cuando el tamaño del modelo y los datos aumenta.

Cada desafío ha dado lugar a la creación de nuevos algoritmos, y la competencia por encontrar mejores algoritmos continúa hasta hoy.

Historia de los algoritmos de optimización

• 1847, Cauchy: Propuso el descenso del gradiente (Gradient Descent). Esta idea simple pero poderosa de ajustar ligeramente los parámetros siguiendo la pendiente (gradient) de la función de pérdida se convirtió en la base del aprendizaje profundo moderno.
• 1951, Robbins y Monro: Establecieron las bases matemáticas del descenso del gradiente estocástico (Stochastic Gradient Descent, SGD). El SGD mejoró significativamente la eficiencia computacional al usar mini-lotes (mini-batch) en lugar de todo el conjunto de datos.
• 1986, Rumelhart: Propuso el método de momentum junto con el algoritmo de retropropagación (Backpropagation). El momentum introduce inercia al proceso de optimización, lo que reduce las oscilaciones del SGD y mejora la velocidad de convergencia.
• 2011, Duchi: Presentó el algoritmo AdaGrad. AdaGrad fue pionero en el ajuste adaptativo de la tasa de aprendizaje para cada parámetro.
• 2012, Hinton: Propuso RMSProp. (Introducido en notas de clase, no publicado en un paper) RMSProp mejoró el problema de disminución de la tasa de aprendizaje en AdaGrad, permitiendo un aprendizaje más estable.
• 2014, Kingma y Ba: Presentaron Adam (Adaptive Moment Estimation). Adam combina las ventajas del momentum y RMSProp, convirtiéndose en uno de los algoritmos de optimización más ampliamente utilizados actualmente.

Los algoritmos de optimización recientes están evolucionando en tres direcciones principales. 1. Eficiencia de memoria: Lion, AdaFactor, entre otros, se centran en reducir el uso de memoria necesario para entrenar modelos a gran escala (especialmente basados en Transformer). 2. Optimización del aprendizaje distribuido: LAMB, LARS, entre otros, mejoran la eficiencia al entrenar modelos a gran escala en paralelo utilizando múltiples GPU/TPU. 3. Optimización especializada por dominio/tarea: Sophia, AdaBelief, entre otros, proporcionan un rendimiento optimizado para áreas de problema específicas (por ejemplo, procesamiento de lenguaje natural, visión por computadora) o estructuras de modelo específicas.

Especialmente con el surgimiento de modelos de lenguaje a gran escala (LLM) y modelos multimodales, se ha vuelto más importante optimizar eficientemente cientos de millones, incluso billones de parámetros, entrenar en entornos de memoria limitada y converger de manera estable en entornos distribuidos. Estos desafíos han llevado al surgimiento de nuevas técnicas como la optimización de 8 bits, ZeRO optimization, gradient checkpointing, entre otras.

Algoritmos de optimización básicos

En el aprendizaje profundo, los algoritmos de optimización desempeñan un papel crucial al buscar el mínimo del función de pérdida, es decir, encontrar los parámetros óptimos del modelo. Cada algoritmo tiene características y ventajas únicas, y es importante seleccionar el algoritmo adecuado según las características del problema y la estructura del modelo.

SGD y momentum

El descenso de gradiente estocástico (Stochastic Gradient Descent, SGD) es un algoritmo de optimización básico y ampliamente utilizado. En cada paso, utiliza datos de mini-lote (mini-batch) para calcular el gradiente de la función de pérdida y actualiza los parámetros en la dirección opuesta.

• Fórmula de actualización de parámetros:

  \[w^{(t)} = w^{(t-1)} - \eta \cdot g^{(t)}\]

  • \(w^{(t)}\): parámetro (peso) en el paso \(t\)
  • \(\eta\): tasa de aprendizaje (learning rate)
  • \(g^{(t)}\): gradiente calculado en el paso \(t\)

El momentum introduce el concepto de inercia del movimiento físico para mejorar SGD. Utiliza la media móvil exponencial (exponential moving average) de los gradientes pasados para otorgar inercia a la trayectoria de optimización, mitigando así el problema de oscilación en SGD y aumentando la velocidad de convergencia.

• Fórmula de actualización con momentum:

  \[v^{(t)} = \mu \cdot v^{(t-1)} + g^{(t)}\]

  \[w^{(t)} = w^{(t-1)} - \eta \cdot v^{(t)}\]

  • \(\mu\): coeficiente de momentum (generalmente 0.9 o 0.99)
  • \(v^{(t)}\): velocidad en el paso \(t\)

El código de implementación de los principales algoritmos de optimización utilizados en el aprendizaje se incluye en el directorio chapter_05/optimizer/. A continuación, se muestra un ejemplo de implementación para el algoritmo SGD (incluyendo momentum) utilizado en el aprendizaje. Todas las clases de algoritmos de optimización heredan de la clase BaseOptimizer y se implementan de manera simple con fines de aprendizaje. (En bibliotecas reales como PyTorch, estas implementaciones son más complejas para mayor eficiencia y generalización.)

from typing import Iterable, List, Optional
from dldna.chapter_05.optimizers.basic import BaseOptimizer

class SGD(BaseOptimizer):
    """Implements SGD with momentum."""
    def __init__(self, params: Iterable[nn.Parameter], lr: float, 
                 maximize: bool = False, momentum: float = 0.0):
        super().__init__(params, lr)
        self.maximize = maximize
        self.momentum = momentum
        self.momentum_buffer_list: List[Optional[torch.Tensor]] = [None] * len(self.params)

    @torch.no_grad()
    def step(self) -> None:
        for i, p in enumerate(self.params):
            grad = p.grad if not self.maximize else -p.grad

            if self.momentum != 0.0:
                buf = self.momentum_buffer_list[i]
                if buf is None:
                    buf = torch.clone(grad).detach()
                else:
                    buf.mul_(self.momentum).add_(grad, alpha=1-self.momentum)
                grad = buf
                self.momentum_buffer_list[i] = buf

            p.add_(grad, alpha=-self.lr)

Algoritmos de tasa de aprendizaje adaptativa (Adaptive Learning Rate Algorithms)

Los parámetros del modelo de aprendizaje profundo se actualizan con frecuencias e importancias diferentes. Los algoritmos de tasa de aprendizaje adaptativa ajustan la tasa de aprendizaje individualmente para cada parámetro, teniendo en cuenta sus características específicas.

• AdaGrad (Adaptive Gradient, 2011):

  • Idea principal: Aplica una tasa de aprendizaje pequeña a los parámetros que se actualizan con frecuencia y una tasa de aprendizaje grande a los parámetros que se actualizan raramente.

  • Fórmula:

    \(w^{(t)} = w^{(t-1)} - \frac{\eta}{\sqrt{G^{(t)} + \epsilon}} \cdot g^{(t)}\)

    • \(G^{(t)}\): suma acumulativa de los cuadrados de los gradientes pasados
    • \(\epsilon\): pequeña constante para evitar la división por cero (por ejemplo: \(10^{-8}\))

  • Ventajas: Es efectivo al tratar con datos dispersos (sparse data).

  • Desventajas: La tasa de aprendizaje disminuye monótonamente a medida que avanza el entrenamiento, lo que puede hacer que el aprendizaje se detenga prematuramente.

• RMSProp (Root Mean Square Propagation, 2012):

  • Idea principal: Para resolver el problema de la disminución de la tasa de aprendizaje en AdaGrad, utiliza una media móvil exponencial (exponential moving average) de los cuadrados de los gradientes pasados en lugar de su suma.

  • Fórmula:

    \(v^{(t)} = \beta \cdot v^{(t-1)} + (1-\beta) \cdot (g^{(t)})^2\)

    \(w^{(t)} = w^{(t-1)} - \frac{\eta}{\sqrt{v^{(t)} + \epsilon}} \cdot g^{(t)}\)

    • \(\beta\): tasa de decaimiento (decay rate) que ajusta la influencia de los cuadrados de los gradientes pasados (generalmente 0.9)

  • Ventajas: El problema de disminución de la tasa de aprendizaje es menos pronunciado en comparación con AdaGrad, permitiendo un entrenamiento efectivo por un período más largo.

Adam (Adaptive Moment Estimation, 2014):

Adam es uno de los algoritmos de optimización más utilizados actualmente, que combina las ideas de momentum y RMSProp.

• Idea principal:

  • Momentum: utiliza una media móvil exponencial del gradiente pasado (primer momento) para introducir un efecto de inercia.
  • RMSProp: utiliza una media móvil exponencial de los cuadrados de los gradientes pasados (segundo momento) para ajustar la tasa de aprendizaje por parámetro.
  • Corrección de sesgo (Bias Correction): corrige el sesgo de los primeros y segundos momentos hacia cero en las etapas iniciales.

• Fórmula:

  \(m^{(t)} = \beta\_1 \cdot m^{(t-1)} + (1-\beta\_1) \cdot g^{(t)}\)

  \(v^{(t)} = \beta\_2 \cdot v^{(t-1)} + (1-\beta\_2) \cdot (g^{(t)})^2\)

  \(\hat{m}^{(t)} = \frac{m^{(t)}}{1-\beta\_1^t}\)

  \(\hat{v}^{(t)} = \frac{v^{(t)}}{1-\beta\_2^t}\)

  \(w^{(t)} = w^{(t-1)} - \eta \cdot \frac{\hat{m}^{(t)}}{\sqrt{\hat{v}^{(t)}} + \epsilon}\)

  • \(\beta_1\): tasa de decaimiento del primer momento (momentum) (generalmente 0.9)
  • \(\beta_2\): tasa de decaimiento del segundo momento (RMSProp) (generalmente 0.999) Los algoritmos de optimización mencionados anteriormente tienen cada uno sus propias ventajas y desventajas, y es necesario elegir el algoritmo adecuado según las características del problema, la estructura del modelo, los datos, etc. Adam muestra un buen rendimiento en muchos casos, pero a veces la combinación de SGD + Momentum puede ofrecer un mejor rendimiento de generalización, o en problemas específicos, otros algoritmos de tasa de aprendizaje adaptativa (por ejemplo: RMSProp) pueden ser más efectivos. Por lo tanto, es importante encontrar el algoritmo óptimo a través de experimentos.

Algoritmos de optimización modernos: más rápidos, más eficientes y para modelos más grandes

Con el aumento explosivo del tamaño de los modelos de aprendizaje profundo y los conjuntos de datos, se ha incrementado la demanda de nuevos algoritmos de optimización que soporten eficiencia en memoria, velocidad de convergencia rápida y aprendizaje distribuido a gran escala. A continuación, se presentan los algoritmos más recientes que han surgido para responder a estas necesidades.

• Lion (Evolved Sign Momentum, 2023):

  • Idea central: Un algoritmo descubierto por Google Research a través de la búsqueda de programas (program search), similar a Adam en el uso del momentum, pero que realiza actualizaciones utilizando solo el signo (sign) de los gradientes. Es decir, ignora la magnitud del gradiente y considera solo su dirección.
  • Ventajas:
    • Utiliza menos memoria que Adam (no requiere almacenar el segundo momento).
    • Realiza actualizaciones del mismo tamaño para todos los parámetros, lo que lo hace efectivo en problemas con gradientes dispersos (por ejemplo, procesamiento de lenguaje natural).
    • Permite utilizar tasas de aprendizaje más altas que Adam.
    • Empíricamente, muestra un mejor rendimiento que AdamW en muchos casos.
  • Desventajas:
    • Ignorar la información de magnitud del gradiente puede resultar en una convergencia más lenta o un rendimiento inferior a Adam en ciertos problemas.
    • Puede ser más sensible al ajuste de la tasa de aprendizaje.
  • Para obtener más detalles, consulte el análisis detallado.

• Sophia (Second-order Clipped Stochastic Optimization, 2023):

  • Idea central: Utiliza información de segundo orden (matriz hessian), pero para reducir los costos computacionales, estima y utiliza solo los componentes diagonales del hessiano y aplica clipping a las actualizaciones para aumentar la estabilidad.
  • Ventajas: Convergencia más rápida y aprendizaje más estable que Adam.
  • Desventajas: Requiere ajustar más hiperparámetros que Adam (por ejemplo, frecuencia de estimación del hessiano, umbral de clipping).
  • Para obtener más detalles, consulte el análisis detallado.

• AdaFactor (2018):

  • Idea central: Algoritmo propuesto para reducir el uso de memoria en modelos a gran escala (especialmente Transformers), que aproxima la matriz del segundo momento en Adam mediante el producto de matrices de baja dimensión.
  • Ventajas: Utiliza significativamente menos memoria que Adam.
  • Desventajas: Debido a la aproximación del segundo momento, puede mostrar un rendimiento inferior a Adam en ciertos problemas.
  • Para obtener más detalles, consulte el análisis detallado.

Investigaciones recientes sugieren que los algoritmos mencionados (Lion, Sophia, AdaFactor) pueden superar el rendimiento de Adam/AdamW existente bajo condiciones específicas.

• Lion: En el aprendizaje con tamaños de lote grandes (large batch size), Lion es más rápido que AdamW, utiliza menos memoria y tiende a mostrar un mejor rendimiento de generalización.
• Sophia: Durante la etapa de pre-entrenamiento (especialmente para modelos de lenguaje a gran escala), Sophia converge más rápidamente que Adam y puede alcanzar una menor perplejidad (o mayor precisión).
• AdaFactor: En entornos con limitaciones de memoria, AdaFactor puede ser una buena alternativa a Adam para entrenar modelos Transformer a gran escala. Sin embargo, no existe un algoritmo de optimización “todo en uno” que garantice siempre el mejor rendimiento para todos los problemas. Por lo tanto, al aplicarlos a problemas reales, es necesario considerar integralmente el tamaño del modelo, las características de los datos de entrenamiento, los recursos disponibles (memoria, potencia de cómputo), si se realizará aprendizaje distribuido, etc., para seleccionar un algoritmo adecuado y necesariamente encontrar los hiperparámetros óptimos a través de experimentos y validación.

Ahora vamos a realizar una prueba de 1 época para ver cómo funciona.

import torch
import torch.nn as nn
from dldna.chapter_04.models.base import SimpleNetwork
from dldna.chapter_04.utils.data import get_data_loaders, get_device
from dldna.chapter_05.optimizers.basic import Adam, SGD
from dldna.chapter_05.optimizers.advanced import Lion, Sophia
from dldna.chapter_04.experiments.model_training import train_model  # Corrected import

device = get_device()
model = SimpleNetwork(act_func=nn.ReLU(), hidden_shape=[512, 64]).to(device)

# Initialize SGD optimizer
optimizer = SGD(params=model.parameters(), lr=1e-3, momentum=0.9)

# # Initialize Adam optimizer
# optimizer = Adam(params=model.parameters(), lr=1e-3, beta1=0.9, beta2=0.999, eps=1e-8)

# # Initialize AdaGrad optimizer
# optimizer = AdaGrad(params=model.parameters(), lr=1e-2, eps=1e-10)

# # Initialize Lion optimizer
# optimizer = Lion(params=model.parameters(), lr=1e-4,  betas=(0.9, 0.99), weight_decay=0.0)

# Initialize Sophia optimizer
# optimizer = Sophia(params=model.parameters(), lr=1e-3, betas=(0.965, 0.99), rho=0.04, weight_decay=0.0, k=10)

train_dataloader, test_dataloader = get_data_loaders()

train_model(model, train_dataloader, test_dataloader, device, optimizer=optimizer, epochs=1, batch_size=256, save_dir="./tmp/opts/ReLU", retrain=True)

Starting training for SimpleNetwork-ReLU.

Execution completed for SimpleNetwork-ReLU, Execution time = 7.4 secs

{'epochs': [1],
 'train_losses': [2.2232478597005207],
 'train_accuracies': [0.20635],
 'test_losses': [2.128580910873413],
 'test_accuracies': [0.3466]}

Haga clic para ver el contenido (deep dive: análisis profundo de los algoritmos de optimización modernos)

Análisis profundo de los algoritmos de optimización modernos

Lion (EvoLved Sign Momentum)

Lion es un algoritmo de optimización descubierto por Google Research mediante técnicas de AutoML. Aunque similar a Adam en el uso del momentum, su característica principal es que utiliza solo el signo de los gradientes y no su magnitud.

Idea clave:

• Descenso por Signo: Decide la dirección de actualización utilizando solo el signo de los gradientes. Esto fuerza una actualización de tamaño uniforme para todos los parámetros, lo que resulta efectivo en problemas con gradientes dispersos (por ejemplo, procesamiento de lenguaje natural).
• Momentum: Considera la dirección de las actualizaciones anteriores para mejorar la estabilidad y velocidad del aprendizaje.

Principios matemáticos:

1. Cálculo de actualización:

   \(c\_t = \beta\_1 m\_{t-1} + (1 - \beta\_1) g\_t\)

   • \(c\_t\): Vector de actualización para el paso actual. Es una media ponderada del momentum (\(m\_{t-1}\)) y el gradiente actual (\(g\_t\)).
   • \(\beta\_1\): Tasa de decay exponencial del momentum (generalmente 0.9 o 0.99).

2. Actualización de pesos:

   \(w\_{t+1} = w\_t - \eta \cdot \text{sign}(c\_t)\)

   • \(\eta\): Tasa de aprendizaje
   • \(\text{sign}(c\_t)\): El signo (+1 o -1) de cada elemento de \(c\_t\). Si es 0, se mantiene como 0.

3. Actualización del momentum:

   \(m\_t = c\_t\)

   • Se utiliza el valor calculado en la actualización para el siguiente paso del momentum.

Ventajas:

• Eficiencia de memoria: A diferencia de Adam, no necesita almacenar el segundo momento (varianza), lo que reduce el uso de memoria.
• Eficiencia computacional: La operación de signo es menos costosa en términos de cálculo que la multiplicación.
• Robustez a la dispersidad: Al actualizar todos los parámetros con un tamaño uniforme, resulta efectivo en problemas con gradientes dispersos.

Desventajas:

• Ignora la información de magnitud del gradiente, lo que puede resultar en una convergencia más lenta o un rendimiento inferior a Adam en ciertos problemas.
• Puede ser más sensible al ajuste de la tasa de aprendizaje.

Referencias:

• Se ha analizado que Lion tiene efectos similares a la regularización L1. (Se requiere investigación adicional para detalles)
• El artículo Chen et al., 2023 informa que, durante el entrenamiento del modelo BERT, Lion mostró una mejora en la tasa de aprendizaje y la estabilidad. Sin embargo, estos resultados son específicos del experimento y no pueden generalizarse a todos los casos.

Sophia (Optimización Estocástica de Segundo Orden Recortada)

Sophia es un algoritmo de optimización que utiliza información de segundo orden (la matriz Hessiana) para mejorar la velocidad y estabilidad del aprendizaje. Sin embargo, el cálculo directo de la matriz Hessiana es muy costoso, por lo que Sophia estima solo los componentes diagonales de la Hessiana mediante una versión mejorada del método de Hutchinson.

Idea clave:

• Estimación ligera de la Hessiana: Mejora el método de Hutchinson para estimar eficientemente los componentes diagonales de la matriz Hessiana.
  • El método de Hutchinson original utiliza \(h\_t = \mathbb{E}[z\_t z\_t^T H\_t] = diag(H\_t)\), donde ( z ) es un vector aleatorio.
  • Mejora: Utiliza covarianza para reducir la varianza.
• Recorte (Clipping): Limita el tamaño de la actualización antes de aplicar los gradientes para mejorar la estabilidad del aprendizaje.

Principios matemáticos: 1. Estimación de la Diagonal de Hessian:

  * En cada paso, se muestrea un vector aleatorio $z\_t$ (cada elemento de $z\_t$ se selecciona uniformemente de {-1, +1}).

  * Se calcula la estimación de la diagonal de Hessian $h\_t$ de la siguiente manera.

    $h\_t = \beta\_2 h\_{t-1} + (1 - \beta\_2) \text{diag}(H\_t z\_t) z\_t^T$

    (donde $H\_t$ es el Hessian en el paso t)

  * Sophia utiliza una media móvil exponencial (EMA) que aprovecha estimaciones pasadas ($h\_{t-1}$) para reducir la varianza del estimador de Hutchinson.

2. Cálculo de la Actualización:

   • \(m\_t = \beta\_1 m\_{t-1} + (1 - \beta\_1) g\_t\) (momentum)
   • \(u\_t = \text{clip}(m\_t / (h\_t + \epsilon), \rho)\)
     • \(u\_t\): actualización recortada después de dividir por el Hessian.
     • \(\text{clip}(x, \rho) = \text{sign}(x) \cdot \min(|x|, \rho)\).
     • \(\rho\): valor umbral de recorte (hiperparámetro)
     • \(h\_t + \epsilon\) es una operación que suma \(\epsilon\) a cada elemento de \(h\_t\)

3. Actualización de Pesos:

   \(w\_{t+1} = w\_t - \eta \cdot u\_t\)

   • \(\eta\): tasa de aprendizaje

Ventajas:

• Convergencia rápida: Utiliza información de segundo orden para converger más rápido que Adam.
• Estabilidad: Mejora la estabilidad del aprendizaje mediante el recorte.

Desventajas:

• Requiere ajustar más hiperparámetros (\(\beta\_1\), \(\beta\_2\), \(\rho\)) en comparación con Adam.
• El rendimiento puede variar según la precisión de la estimación del Hessian.

Referencia:

• Li et al., 2023 informa que Sophia logró una pérdida (loss) más baja en menos pasos de Adam durante el pre-entrenamiento de modelos de lenguaje. (usando métricas como precisión/perplexity)

AdaFactor

AdaFactor es un algoritmo de optimización eficiente en términos de memoria, diseñado para el entrenamiento de modelos a gran escala, especialmente los modelos Transformer. Aunque similar a Adam en su uso de tasas de aprendizaje adaptativas, mejora la forma de almacenar el segundo momento (varianza), reduciendo significativamente el consumo de memoria.

Idea clave:

• Factorización matricial (Matrix Factorization): Aproxima la matriz del segundo momento como el producto de dos matrices de baja dimensión para reducir el uso de memoria.

Principio matemático:

En Adam, la matriz del segundo momento \(v\_t\) para una matriz de pesos de tamaño \(n \times m\) requiere \(O(nm)\) de memoria. AdaFactor aproxima esta matriz de la siguiente manera.

1. Estimación del Segundo Momento:

• En lugar de \(v\_t\), mantenemos dos vectores \(R\_t\) (\(n \times 1\)) y \(C\_t\) (\(m \times 1\)) que representan la suma de cada fila y columna de \(v\_t\).
  • \(R\_t = \beta\_{2t} R\_{t-1} + (1 - \beta\_{2t}) (\text{row\_sum}(g\_t^2)/m)\)
  • \(C\_t = \beta\_{2t} C\_{t-1} + (1 - \beta\_{2t}) (\text{col\_sum}(g\_t^2)/n)\)
• \(R\_t\) y \(C\_t\) son valores de media móvil exponencial (exponential moving average) de la suma de las filas y columnas de \(g\_t^2\), respectivamente. (\(\beta\_{2t}\) es el horizonte de planificación)
• Aproximamos \(\hat{v\_t} = R\_t C\_t^T / (\text{sum}(R\_t) \cdot \text{sum}(C\_t))\)

2. Cálculo de la actualización:

   \(u\_t = g\_t / \sqrt{\hat{v\_t}}\)

3. Actualización de los pesos \(w\_{t+1} = w\_t - \eta \cdot u\_t\)

Ventajas:

• Eficiencia de memoria: En lugar de almacenar una matriz de segundo momento de tamaño \(O(nm)\), solo almacenamos vectores de tamaño \(O(n+m)\), lo que reduce significativamente el uso de memoria.
• Aprendizaje de modelos grandes: Debido a la eficiencia en el uso de memoria, es adecuado para el aprendizaje de modelos de gran escala.

Desventajas:

• Dado que se aproxima la información del segundo momento, en ciertos problemas puede tener un rendimiento inferior al de Adam.
• Puede incurrir en costos computacionales adicionales debido a la descomposición matricial.

Referencia:

• Shazeer & Stern, 2018 informan que AdaFactor logra un rendimiento similar al de Adam mientras reduce el uso de memoria en el aprendizaje de modelos de transformers.

Otros algoritmos de optimización relevantes y recientes

• LAMB (Layer-wise Adaptive Moments optimizer for Batch training): Un algoritmo especializado para el aprendizaje con lotes grandes. Ajusta la tasa de aprendizaje por capa, permitiendo un aprendizaje estable incluso con lotes de gran tamaño. (Referencia: You et al., 2019)
• LARS (Layer-wise Adaptive Rate Scaling): Similar a LAMB, utiliza ajustes de tasa de aprendizaje por capa y es efectivo para el aprendizaje con lotes grandes. Se usa principalmente en modelos de clasificación de imágenes como ResNet. (Referencia: You et al., 2017)

5.2.2 Comparación de entrenamiento de optimización

El rendimiento del algoritmo de optimización puede variar significativamente según la tarea y la estructura del modelo. Analizaremos estas características a través de experimentos.

Análisis de tareas básicas

Comparamos el rendimiento básico utilizando el conjunto de datos FashionMNIST. Este conjunto de datos simplifica el problema de clasificación de imágenes de ropa reales, lo que lo hace adecuado para analizar las características básicas de los algoritmos de deep learning.

from dldna.chapter_05.experiments.basic import run_basic_experiment
from dldna.chapter_05.visualization.optimization import plot_training_results
from dldna.chapter_04.utils.data import get_data_loaders
from dldna.chapter_05.optimizers.basic import SGD, Adam
from dldna.chapter_05.optimizers.advanced import Lion
import torch

# Device configuration
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")


# Data loaders
train_loader, test_loader = get_data_loaders()

# Optimizer dictionary
optimizers = {
    'SGD': SGD,
    'Adam': Adam,
    'Lion': Lion
}

# Optimizer configurations
optimizer_configs = {
    'SGD': {'lr': 0.01, 'momentum': 0.9},
    'Adam': {'lr': 0.001},
    'Lion': {'lr': 1e-4}
}

# Run experiments
results = {}
for name, config in optimizer_configs.items():
    print(f"\nStarting experiment with {name} optimizer...")
    results[name] = run_basic_experiment(
        optimizer_class=optimizers[name],
        train_loader=train_loader,
        test_loader=test_loader,
        config=config,
        device=device,
        epochs=20
    )

# Visualize training curves
plot_training_results(
    results,
    metrics=['loss', 'accuracy', 'gradient_norm', 'memory'],
    mode="train",  # Changed mode to "train"
    title='Optimizer Comparison on FashionMNIST'
)

Starting experiment with SGD optimizer...

==================================================
Optimizer: SGD
Initial CUDA Memory Status (GPU 0):
Allocated: 23.0MB
Reserved: 48.0MB
Model Size: 283.9K parameters
==================================================

==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 27.2MB
Peak Reserved: 48.0MB
Current Allocated: 25.2MB
Current Reserved: 48.0MB
==================================================


Starting experiment with Adam optimizer...

==================================================
Optimizer: Adam
Initial CUDA Memory Status (GPU 0):
Allocated: 25.2MB
Reserved: 48.0MB
Model Size: 283.9K parameters
==================================================

==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 28.9MB
Peak Reserved: 50.0MB
Current Allocated: 26.3MB
Current Reserved: 50.0MB
==================================================


Starting experiment with Lion optimizer...

==================================================
Optimizer: Lion
Initial CUDA Memory Status (GPU 0):
Allocated: 24.1MB
Reserved: 50.0MB
Model Size: 283.9K parameters
==================================================

==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 27.2MB
Peak Reserved: 50.0MB
Current Allocated: 25.2MB
Current Reserved: 50.0MB
==================================================

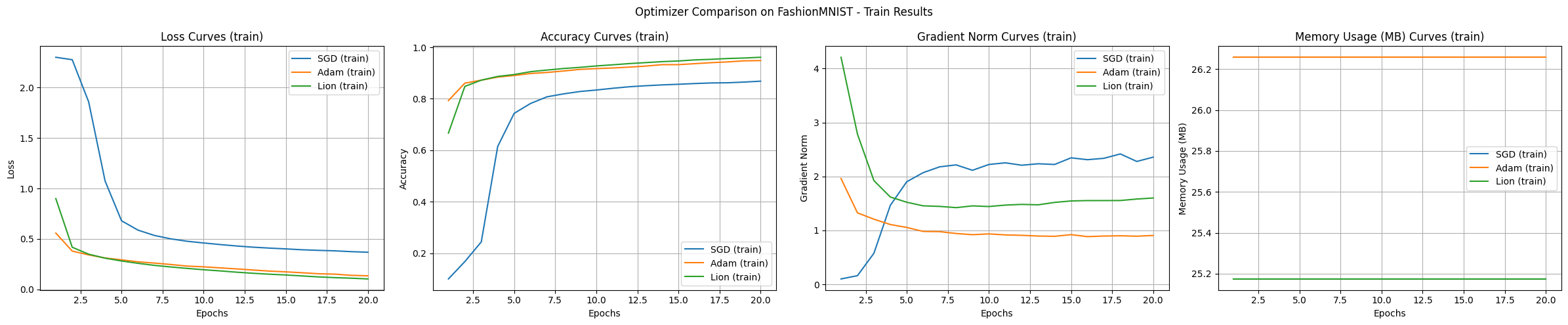
Los resultados del experimento muestran las características de cada algoritmo. En el experimento realizado con el conjunto de datos FashionMNIST y el modelo MLP, los principales hallazgos son los siguientes:

1. Velocidad de convergencia:
   • Adam y Lion convergen muy rápidamente en las primeras etapas del aprendizaje. (disminución rápida de la pérdida y aumento rápido de la precisión en los primeros pocos episodios)
   • SGD muestra un patrón de convergencia más lento y constante.
2. Estabilidad de la curva de aprendizaje:
   • Adam presenta una curva de aprendizaje muy suave y estable.
   • Lion es similar a Adam en estabilidad, pero presenta algunas fluctuaciones en la curva de precisión.
   • SGD muestra grandes fluctuaciones tanto en las curvas de pérdida como de precisión.
3. Uso de memoria:
   • Lion utiliza ligeramente menos memoria que Adam, aunque no hay una gran diferencia (Adam: aproximadamente 26.2MB, Lion: aproximadamente 25.2MB).
   • SGD es el que consume la menor cantidad de memoria entre los tres.
4. Norma del gradiente:
   • Lion: La norma del gradiente inicial es muy alta (aproximadamente 4.0) y disminuye rápidamente, estabilizándose en un valor bajo (aproximadamente 1.5). (exploración de grandes pasos iniciales, movimiento rápido hacia el óptimo)
   • Adam: La norma del gradiente inicial es menor que la de Lion (aproximadamente 2.0), disminuye rápidamente y se estabiliza en un valor aún más bajo (aproximadamente 1.0). (ajuste adaptativo de la tasa de aprendizaje)
   • SGD: La norma del gradiente inicial es la menor (aproximadamente 0.3), presenta grandes fluctuaciones y oscila a valores más altos (aproximadamente 2.0-2.5) en comparación con los otros algoritmos. (exploración de un amplio área, posibilidad de mínimos planos)

En el experimento básico, Adam y Lion mostraron una rápida velocidad de convergencia inicial, Adam presentó el aprendizaje más estable, Lion utilizó ligeramente menos memoria, y SGD tendía a explorar un rango más amplio.

Evaluación de tareas avanzadas

Con CIFAR-100 y modelos CNN/transformer, las diferencias entre los algoritmos de optimización se vuelven aún más evidentes.

from dldna.chapter_05.experiments.advanced import run_advanced_experiment
from dldna.chapter_05.visualization.optimization import plot_training_results
from dldna.chapter_04.utils.data import get_data_loaders
from dldna.chapter_05.optimizers.basic import SGD, Adam
from dldna.chapter_05.optimizers.advanced import Lion
import torch

# Device configuration
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# Data loaders
train_loader, test_loader = get_data_loaders(dataset="CIFAR100")

# Optimizer dictionary
optimizers = {
    'SGD': SGD,
    'Adam': Adam,
    'Lion': Lion
}

# Optimizer configurations
optimizer_configs = {
    'SGD': {'lr': 0.01, 'momentum': 0.9},
    'Adam': {'lr': 0.001},
    'Lion': {'lr': 1e-4}
}

# Run experiments
results = {}
for name, config in optimizer_configs.items():
    print(f"\nStarting experiment with {name} optimizer...")
    results[name] = run_advanced_experiment(
        optimizer_class=optimizers[name],
        model_type='cnn',
        train_loader=train_loader,
        test_loader=test_loader,
        config=config,
        device=device,
        epochs=40
    )

# Visualize training curves
plot_training_results(
    results,
    metrics=['loss', 'accuracy', 'gradient_norm', 'memory'],
    mode="train",
    title='Optimizer Comparison on CIFAR100'
)

Files already downloaded and verified
Files already downloaded and verified

Starting experiment with SGD optimizer...

==================================================
Optimizer: SGD
Initial CUDA Memory Status (GPU 0):
Allocated: 26.5MB
Reserved: 50.0MB
Model Size: 1194.1K parameters
==================================================

==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 120.4MB
Peak Reserved: 138.0MB
Current Allocated: 35.6MB
Current Reserved: 138.0MB
==================================================

Results saved to: SGD_cnn_20250225_161620.csv

Starting experiment with Adam optimizer...

==================================================
Optimizer: Adam
Initial CUDA Memory Status (GPU 0):
Allocated: 35.6MB
Reserved: 138.0MB
Model Size: 1194.1K parameters
==================================================

==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 124.9MB
Peak Reserved: 158.0MB
Current Allocated: 40.2MB
Current Reserved: 158.0MB
==================================================

Results saved to: Adam_cnn_20250225_162443.csv

Starting experiment with Lion optimizer...

==================================================
Optimizer: Lion
Initial CUDA Memory Status (GPU 0):
Allocated: 31.0MB
Reserved: 158.0MB
Model Size: 1194.1K parameters
==================================================

==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 120.4MB
Peak Reserved: 158.0MB
Current Allocated: 35.6MB
Current Reserved: 158.0MB
==================================================

Results saved to: Lion_cnn_20250225_163259.csv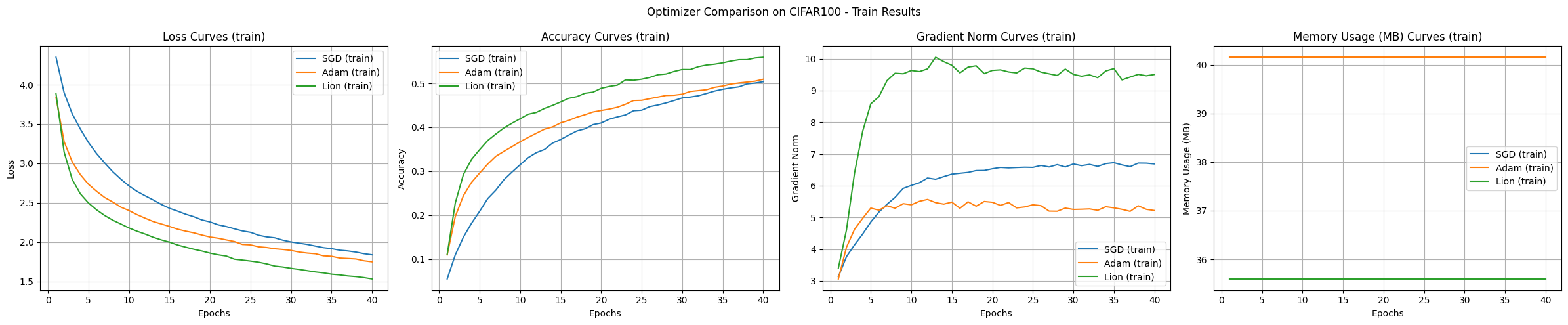

Los resultados del experimento comparan los algoritmos de optimización SGD, Adam y Lion utilizando el conjunto de datos CIFAR-100 y un modelo CNN, mostrando las características de cada algoritmo.

1. Velocidad de convergencia y precisión:

   • SGD muestra una baja precisión (inferior a aproximadamente 50%) incluso después de 40 épocas, convergiendo lentamente.
   • Adam alcanza una precisión de aproximadamente 50% alrededor de las 20 épocas, convergiendo relativamente rápido.
   • Lion converge más rápidamente que Adam y logra la mayor precisión de aproximadamente 55% en 40 épocas.

2. Estabilidad de la curva de aprendizaje:

   • Adam es estable tanto en las curvas de Loss como de Accuracy.
   • Lion es similarmente estable a Adam, aunque presenta alguna variación en la curva de Accuracy.
   • SGD muestra alta variabilidad tanto en las curvas de Loss como de Accuracy.

3. Uso de memoria:

   • Lion (aproximadamente 31MB) y SGD (aproximadamente 31MB) utilizan menos memoria que Adam (aproximadamente 34MB).

4. Norma del gradiente:

   • Lion: La norma del gradiente inicial es alta (aproximadamente 3.56), aumenta rápidamente y luego disminuye, estabilizándose alrededor de 10. (exploración con grandes pasos iniciales)
   • Adam: La norma del gradiente inicial es menor que la de Lion (aproximadamente 3.26), aumenta gradualmente y se estabiliza. (exploración estable)
   • SGD: La norma del gradiente inicial es la más baja (aproximadamente 3.13), muestra alta variabilidad y se mantiene en valores altos en comparación con los otros algoritmos.

Dadas las condiciones experimentales, Lion mostró la velocidad de convergencia más rápida y la mayor precisión. Adam presentó curvas de aprendizaje estables, mientras que SGD fue lento y variable. En términos de uso de memoria, Lion y SGD utilizaron menos memoria que Adam.

from dldna.chapter_05.experiments.advanced import run_advanced_experiment
from dldna.chapter_05.visualization.optimization import plot_training_results
from dldna.chapter_04.utils.data import get_data_loaders
from dldna.chapter_05.optimizers.basic import SGD, Adam
from dldna.chapter_05.optimizers.advanced import Lion
import torch

# Device configuration
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# Data loaders
train_loader, test_loader = get_data_loaders(dataset="CIFAR100")

# Optimizer dictionary
optimizers = {
    'SGD': SGD,
    'Adam': Adam,
    'Lion': Lion
}

# Optimizer configurations
optimizer_configs = {
    'SGD': {'lr': 0.01, 'momentum': 0.9},
    'Adam': {'lr': 0.001},
    'Lion': {'lr': 1e-4}
}

# Run experiments
results = {}
for name, config in optimizer_configs.items():
    print(f"\nStarting experiment with {name} optimizer...")
    results[name] = run_advanced_experiment(
        optimizer_class=optimizers[name],
        model_type='transformer',
        train_loader=train_loader,
        test_loader=test_loader,
        config=config,
        device=device,
        epochs=40
    )

# Visualize training curves
plot_training_results(
    results,
    metrics=['loss', 'accuracy', 'gradient_norm', 'memory'],
    mode="train",
    title='Optimizer Comparison on CIFAR100'
)

Files already downloaded and verified
Files already downloaded and verified

Starting experiment with SGD optimizer...

/home/sean/anaconda3/envs/DL/lib/python3.10/site-packages/torch/nn/modules/transformer.py:379: UserWarning: enable_nested_tensor is True, but self.use_nested_tensor is False because encoder_layer.norm_first was True
  warnings.warn(

==================================================
Optimizer: SGD
Initial CUDA Memory Status (GPU 0):
Allocated: 274.5MB
Reserved: 318.0MB
Model Size: 62099.8K parameters
==================================================

==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 836.8MB
Peak Reserved: 906.0MB
Current Allocated: 749.5MB
Current Reserved: 906.0MB
==================================================

Results saved to: SGD_transformer_20250225_164652.csv

Starting experiment with Adam optimizer...

==================================================
Optimizer: Adam
Initial CUDA Memory Status (GPU 0):
Allocated: 748.2MB
Reserved: 906.0MB
Model Size: 62099.8K parameters
==================================================

==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 1073.0MB
Peak Reserved: 1160.0MB
Current Allocated: 985.1MB
Current Reserved: 1160.0MB
==================================================

Results saved to: Adam_transformer_20250225_170159.csv

Starting experiment with Lion optimizer...

==================================================
Optimizer: Lion
Initial CUDA Memory Status (GPU 0):
Allocated: 511.4MB
Reserved: 1160.0MB
Model Size: 62099.8K parameters
==================================================

==================================================
Final CUDA Memory Status (GPU 0):
Peak Allocated: 985.1MB
Peak Reserved: 1160.0MB
Current Allocated: 748.2MB
Current Reserved: 1160.0MB
==================================================

Results saved to: Lion_transformer_20250225_171625.csv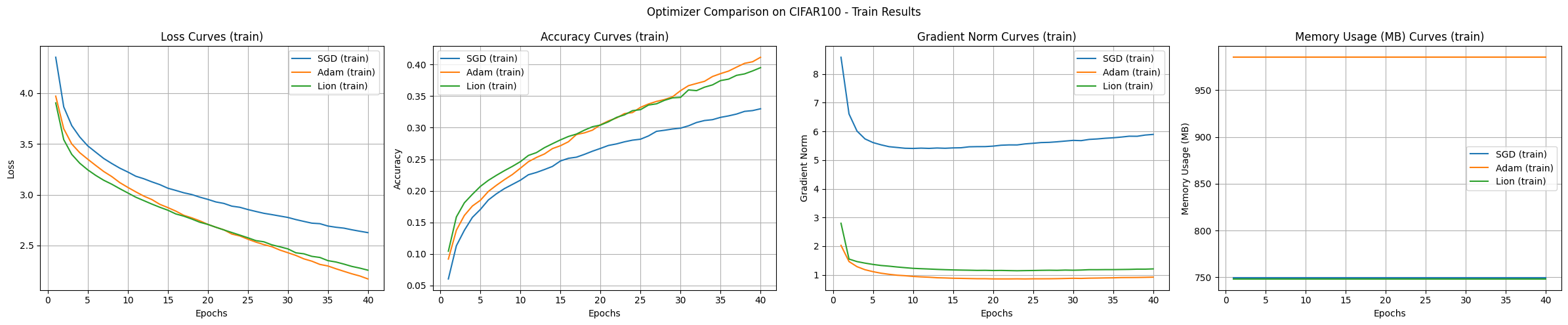

Generalmente, los transformadores se utilizan más en forma de estructuras adaptadas a las características de las imágenes, como el ViT (Vision Transformer), en lugar de aplicarse directamente a tareas de clasificación de imágenes. Este experimento se lleva a cabo como un ejemplo para comparar algoritmos de optimización. Los resultados del experimento del modelo de transformador son los siguientes.

1. Rendimiento de convergencia: Adam muestra la convergencia inicial más rápida, seguido por Lion y SGD.
2. Estabilidad y generalización: Adam alcanza el 30.5% y muestra el rendimiento más estable. Lion alcanza una precisión de prueba del 28.88%, con una ligera disminución en el rendimiento en la etapa final del entrenamiento. SGD logra un 31.1% de precisión, mostrando el mejor rendimiento de generalización.
3. Uso de memoria: Lion y SGD usan cantidades similares de memoria, mientras que Adam usa relativamente más memoria.
4. Dinámica del gradiente: La norma del gradiente de Adam disminuye gradualmente de 1.98 a 0.92. Lion comienza en 2.81 y disminuye hasta 1.21, mientras que SGD comienza en 8.41 y disminuye hasta 5.92, mostrando el cambio más significativo.

Conclusión Los resultados del experimento con el conjunto de datos CIFAR-100 muestran que SGD presenta el mejor rendimiento de generalización, aunque es el más lento en términos de velocidad de aprendizaje. Adam muestra la convergencia más rápida y un aprendizaje estable, pero consume mucha memoria, mientras que Lion demuestra un rendimiento equilibrado en términos de eficiencia de memoria y velocidad de convergencia.

5.3 Visualización y análisis del proceso de optimización: Mirando dentro de la caja negra del aprendizaje profundo

Desafío: ¿Cómo podemos visualizar y comprender eficazmente el proceso de optimización de redes neuronales en espacios de alta dimensión, con millones o incluso decenas de millones de dimensiones?

Lamentaciones del investigador: El espacio de parámetros de los modelos de aprendizaje profundo es un espacio de ultra-alta dimensión que resulta difícil de imaginar intuitivamente para los humanos. A pesar de los esfuerzos de los investigadores por desarrollar diversas técnicas de reducción de dimensionalidad y herramientas de visualización para abrir esta “caja negra”, aún hay muchas áreas que permanecen veladas.

Entender el proceso de aprendizaje de las redes neuronales es fundamental para diseñar modelos eficaces, seleccionar algoritmos de optimización y ajustar hiperparámetros. En particular, visualizar y analizar la geometría de la función de pérdida (loss function) y la trayectoria de optimización proporciona importantes insights sobre la dinámica del proceso de aprendizaje y su estabilidad. En los últimos años, la investigación en la visualización de superficies de pérdida ha brindado pistas clave a los investigadores de aprendizaje profundo para desentrañar los misterios del aprendizaje de redes neuronales, contribuyendo al desarrollo de algoritmos y arquitecturas de modelos más eficientes y estables.

En esta sección, examinaremos los conceptos básicos y las técnicas más recientes en la visualización de superficies de pérdida, y cómo estas pueden ayudarnos a analizar diversos fenómenos que ocurren durante el proceso de aprendizaje en redes neuronales (por ejemplo: mínimos locales, puntos de silla, características de la trayectoria de optimización). En particular, nos centraremos en cómo la estructura del modelo (por ejemplo, conexiones residuales) afecta a la superficie de pérdida y las diferencias en la trayectoria de optimización según el algoritmo de optimización utilizado.

5.3.1 Comprensión de la Superficie de Pérdida (Loss Landscape): El mapa topográfico del modelo de aprendizaje profundo

La visualización de la superficie de pérdida es una herramienta clave para comprender el proceso de aprendizaje en modelos de aprendizaje profundo. Al igual que un mapa topográfico nos permite entender las altitudes y depresiones de un paisaje, la visualización de la superficie de pérdida nos permite visualizar los cambios de la función de pérdida en el espacio de parámetros.

En 2017, Goodfellow et al. demostraron que la planitud (flatness) de la superficie de pérdida está estrechamente relacionada con el rendimiento de generalización del modelo (la tendencia es que los mínimos anchos y planos tienen un mejor rendimiento de generalización que los mínimos estrechos y afilados). En 2018, Li et al. mostraron mediante visualizaciones tridimensionales que las conexiones residuales (residual connections) aplanan la superficie de pérdida, facilitando el aprendizaje. Estos descubrimientos han sido fundamentales en el diseño de arquitecturas modernas de redes neuronales como ResNet.

Técnicas básicas de visualización

1. Interpolación Lineal (Linear Interpolation):

   • Concepto: Se combinan linealmente los pesos de dos modelos diferentes (por ejemplo, un modelo antes y después del aprendizaje, o modelos que convergen a diferentes mínimos locales) para calcular el valor de la función de pérdida entre ellos.

   • Fórmula:

     \(w(\alpha) = (1-\alpha)w_1 + \alpha w_2\)

     • \(w_1\), \(w_2\): pesos de los dos modelos
     • \(\alpha \in [0,1]\): coeficiente de interpolación (0 para \(w_1\), 1 para \(w_2\), y valores intermedios para combinaciones lineales de los pesos)
     • \(L(w(\alpha))\): valor de pérdida en el peso interpolado \(w(\alpha)\)

import torch
import torch.nn as nn
from torch.utils.data import DataLoader, Subset
from dldna.chapter_05.visualization.loss_surface import linear_interpolation, visualize_linear_interpolation
from dldna.chapter_04.utils.data import get_dataset
from dldna.chapter_04.utils.metrics import load_model

# Linear Interpolation

# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Get the dataset
_, test_dataset = get_dataset(dataset="FashionMNIST")
# Create a small dataset
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

# model1, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="tmp/models/")
# model2, _ = load_model(model_file="SimpleNetwork-Tanh.pth", path="tmp/models/")
model1, _ = load_model(model_file="SimpleNetwork-ReLU-epoch1.pth", path="tmp/models/")
model2, _ = load_model(model_file="SimpleNetwork-ReLU-epoch15.pth", path="tmp/models/")


model1 = model1.to(device)
model2 = model2.to(device)
# Linear interpolation

# Test with a small dataset
_, test_dataset = get_dataset(dataset="FashionMNIST")
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)

alphas, losses,  accuracies = linear_interpolation(model1, model2, data_loader, loss_func, device)

_ = visualize_linear_interpolation(alphas, losses, accuracies,  "ReLU(1)-ReLU(15)",  size=(6, 4))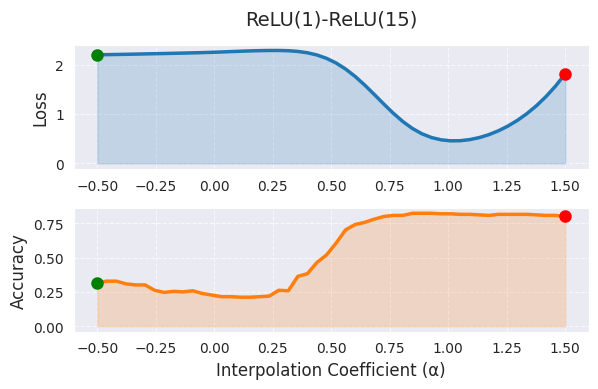

En la interpolación lineal, α=0 representa el primer modelo (1 época de entrenamiento), y α=1 representa el segundo modelo (15 épocas de entrenamiento), mientras que los valores intermedios indican combinaciones lineales de los pesos de ambos modelos. En el gráfico, se observa una tendencia a la disminución de los valores de la función de pérdida a medida que α aumenta, lo cual indica que el modelo se desplaza hacia un mejor óptimo a medida que avanza el entrenamiento. Sin embargo, la interpolación lineal tiene la limitación de mostrar solo una faceta muy restringida del espacio de pesos de alta dimensión. La ruta óptima real entre los dos modelos es probablemente no lineal, y extender el rango de α más allá de [0,1] dificulta su interpretación.

La exploración de rutas no lineales utilizando curvas de Bézier o splines, y la visualización de estructuras de alta dimensión mediante PCA o t-SNE, pueden proporcionar información más completa. En la práctica, se recomienda utilizar la interpolación lineal como herramienta de análisis inicial, y limitar α al rango [0,1] o con una pequeña extrapolación. Es importante analizar de manera integral junto con otras técnicas de visualización, especialmente cuando las diferencias en el rendimiento del modelo son significativas.

A continuación se presentan los análisis de PCA y t-SNE.

import torch
from dldna.chapter_05.visualization.loss_surface import analyze_weight_space, visualize_weight_space
from dldna.chapter_04.utils.metrics import load_model, load_models_by_pattern


models, labels = load_models_by_pattern(
    activation_types=['ReLU'],
    # activation_types=['Tanh'],
    # activation_types=['GELU'],
    epochs=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]
)

# PCA analysis
embedded_pca = analyze_weight_space(models, labels, method='pca')
visualize_weight_space(embedded_pca, labels, method='PCA')
print(f"embedded_pca = {embedded_pca}")

# t-SNE analysis
embedded_tsne = analyze_weight_space(models, labels, method='tsne', perplexity=1)
visualize_weight_space(embedded_tsne, labels, method='t-SNE')
print(f"embedded_tsne = {embedded_tsne}") # Corrected: Print embedded_tsne, not embedded_pca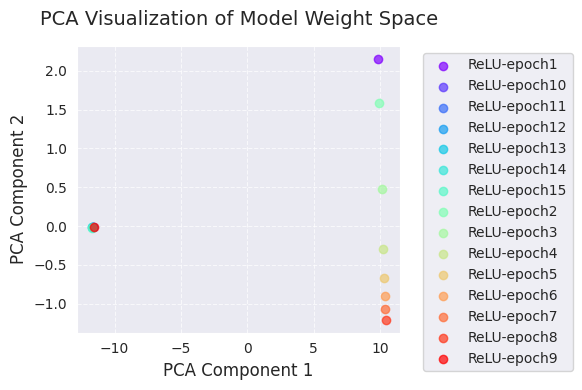

embedded_pca = [[ 9.8299894e+00  2.1538167e+00]
 [-1.1609798e+01 -9.0169059e-03]
 [-1.1640446e+01 -1.2218434e-02]
 [-1.1667191e+01 -1.3469303e-02]
 [-1.1691980e+01 -1.5136327e-02]
 [-1.1714937e+01 -1.6765745e-02]
 [-1.1735878e+01 -1.8110925e-02]
 [ 9.9324265e+00  1.5862983e+00]
 [ 1.0126298e+01  4.7935897e-01]
 [ 1.0256655e+01 -2.8844318e-01]
 [ 1.0319887e+01 -6.6510278e-01]
 [ 1.0359785e+01 -8.9812231e-01]
 [ 1.0392080e+01 -1.0731999e+00]
 [ 1.0418671e+01 -1.2047548e+00]
 [-1.1575559e+01 -5.1336871e-03]]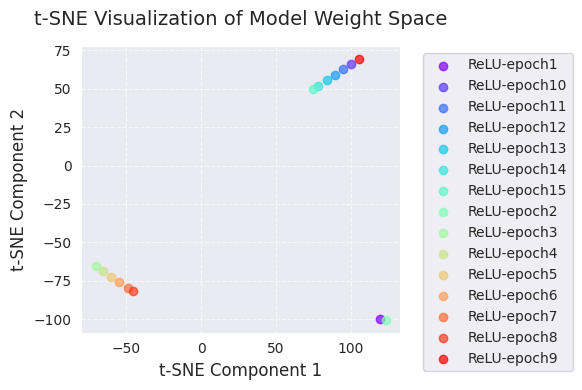

embedded_tsne = [[ 119.4719    -99.78837 ]
 [ 100.26558    66.285835]
 [  94.79294    62.795162]
 [  89.221085   59.253677]
 [  83.667984   55.70297 ]
 [  77.897224   52.022995]
 [  74.5897     49.913578]
 [ 123.20351  -100.34615 ]
 [ -70.45423   -65.66194 ]
 [ -65.55417   -68.90429 ]
 [ -60.166885  -72.466805]
 [ -54.70004   -76.077   ]
 [ -49.00131   -79.833694]
 [ -45.727974  -81.99213 ]
 [ 105.22419    69.45333 ]]

La visualización de PCA y t-SNE proyecta los cambios en el espacio de pesos del modelo durante el proceso de aprendizaje a una dimensión más baja (2D).

• Visualización de PCA:
  • Los puntos representan los pesos del modelo para cada época (epoch). (Morado (época 1) -> Rojo (época 9) -> Verde (después de la época 10))
  • Los pesos que se dispersaban ampliamente al principio se agrupan en una región específica a medida que avanza el aprendizaje.
  • En particular, se observa un cambio significativo cuando se pasa de la época 9 a la época 10.
  • PCA muestra las direcciones (componentes principales) donde ocurren los mayores cambios en el espacio de pesos.
• Visualización de t-SNE:
  • Similar a PCA, los colores de los puntos cambian según la época y muestran cómo evoluciona la distribución de los pesos durante las etapas tempranas, medias y tardías del aprendizaje.
  • t-SNE es una técnica de reducción de dimensiones no lineal que se centra en preservar las relaciones de vecindad local en el espacio de alta dimensión.
  • El grupo de épocas 1-9 y el grupo de épocas 10-15 están relativamente bien separados, lo cual respalda los resultados de PCA.

A través de estas visualizaciones, se puede obtener una comprensión intuitiva de cómo cambian los pesos del modelo durante el proceso de aprendizaje y cómo el algoritmo de optimización explora el espacio de pesos. Particularmente, usar PCA y t-SNE juntos permite apreciar tanto los cambios globales (PCA) como las estructuras locales (t-SNE) simultáneamente.

2. Mapa de contorno (Contour Plot)

El mapa de contorno es un método que traza líneas (contornos) que conectan puntos donde el valor de la función de pérdida es constante en un plano bidimensional, para visualizar la forma de la superficie de pérdida. Al igual que las líneas de contorno en un mapa topográfico, muestra las “elevaciones” de la función de pérdida.

El procedimiento general es el siguiente:

1. Establecimiento del punto de referencia: Se selecciona un conjunto de parámetros del modelo (\(w_0\)) como punto de referencia. (ejemplo: los parámetros de un modelo ya entrenado)

2. Selección de vectores de dirección: Se eligen dos vectores de dirección (\(d_1\), \(d_2\)). Estos vectores forman una base para el plano bidimensional.

   • Elecciones comunes: direcciones aleatorias, direcciones de los componentes principales obtenidas a través de PCA (Análisis de Componentes Principales), o los dos primeros autovectores del tensor Hessiano obtenidos usando bibliotecas como PyHessian. En el último caso, representan las direcciones en las que la función de pérdida cambia más drásticamente.

3. Perturbación de parámetros: Se perturban (varían) los parámetros a lo largo de los dos vectores de dirección seleccionados \(d_1\), \(d_2\) con el punto de referencia \(w_0\) como centro.

   $w(\lambda_1, \lambda_2) = w_0 + \lambda_1 d_1 + \lambda_2 d_2$
   
   *   $\lambda_1$, $\lambda_2$: coeficientes escalares para cada vector de dirección (ejemplo: valores seleccionados a intervalos constantes en el rango -0.2 ~ 0.2)

4. Cálculo del valor de pérdida: Para cada combinación \((\lambda_1, \lambda_2)\), se aplican los parámetros perturbados \(w(\lambda_1, \lambda_2)\) al modelo y se calcula el valor de la función de pérdida.

5. Gráfico de contorno: Se traza un gráfico de contorno bidimensional utilizando los datos \((\lambda_1, \lambda_2, L(w(\lambda_1, \lambda_2)))\). (se pueden usar funciones como contour o tricontourf de matplotlib)

El mapa de contorno muestra visualmente la geometría local de la superficie de pérdida y puede utilizarse para analizar el comportamiento de los algoritmos de optimización al mostrar sus trayectorias junto con las líneas de contorno.

import torch
import numpy as np
import torch.nn as nn
from torch.utils.data import DataLoader, Subset
from dldna.chapter_05.visualization.loss_surface import hessian_eigenvectors, xy_perturb_loss, visualize_loss_surface, linear_interpolation
from dldna.chapter_04.utils.data import get_dataset
from dldna.chapter_04.utils.metrics import load_model
from dldna.chapter_05.optimizers.basic import SGD, Adam

# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Get the dataset
_, test_dataset = get_dataset(dataset="FashionMNIST")
# Create a small dataset
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

trained_model, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="tmp/models/")
# trained_model, _ = load_model(model_file="SimpleNetwork-Tanh.pth", path="tmp/models/")

trained_model = trained_model.to(device)


# pyhessian
data = []  # List to store the calculated result sets
top_n = 4  # Must be an even number.  Each pair of eigenvectors is used.  2 is the minimum.  10 means 5 graphs.
top_eigenvalues, top_eignevectors = hessian_eigenvectors(model=trained_model, loss_func=loss_func, data_loader=data_loader, top_n=top_n, is_cuda=True)

# Define the scale with lambda.
lambda1, lambda2 = np.linspace(-0.2, 0.2, 40).astype(np.float32), np.linspace(-0.2, 0.2, 40).astype(np.float32)

# If top_n=10, a total of 5 pairs of graphs can be drawn.
for i in range(top_n // 2):
    x, y, z = xy_perturb_loss(model=trained_model, top_eigenvectors=top_eignevectors[i*2:(i+1)*2], data_loader=data_loader, loss_func=loss_func, lambda1=lambda1, lambda2=lambda2, device=device)
    data.append((x, y, z))

_ = visualize_loss_surface(data, "ReLU", color="C0", alpha=0.6, plot_3d=True)
_ = visualize_loss_surface(data, "ReLU", color="C0", alpha=0.6, plot_3d=False) # Changed "ReLu" to "ReLU" for consistency

/home/sean/anaconda3/envs/DL/lib/python3.10/site-packages/torch/autograd/graph.py:825: UserWarning: Using backward() with create_graph=True will create a reference cycle between the parameter and its gradient which can cause a memory leak. We recommend using autograd.grad when creating the graph to avoid this. If you have to use this function, make sure to reset the .grad fields of your parameters to None after use to break the cycle and avoid the leak. (Triggered internally at ../torch/csrc/autograd/engine.cpp:1201.)
  return Variable._execution_engine.run_backward(  # Calls into the C++ engine to run the backward pass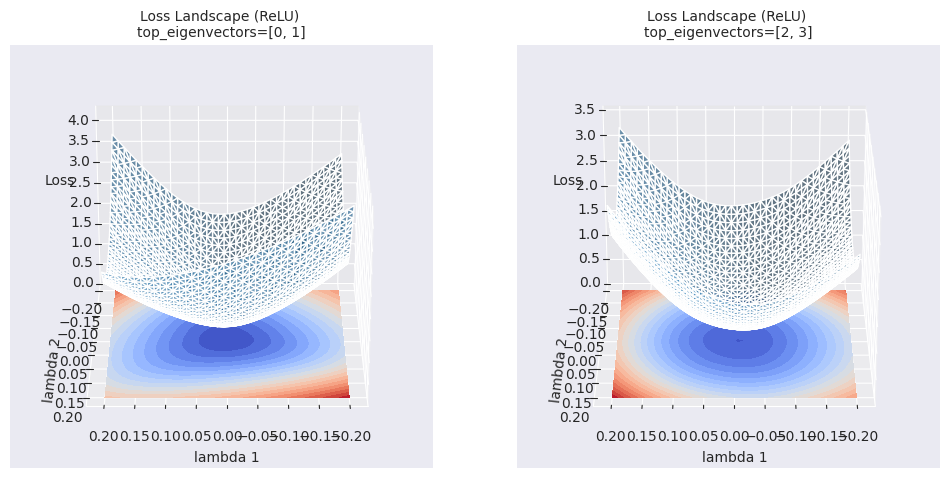

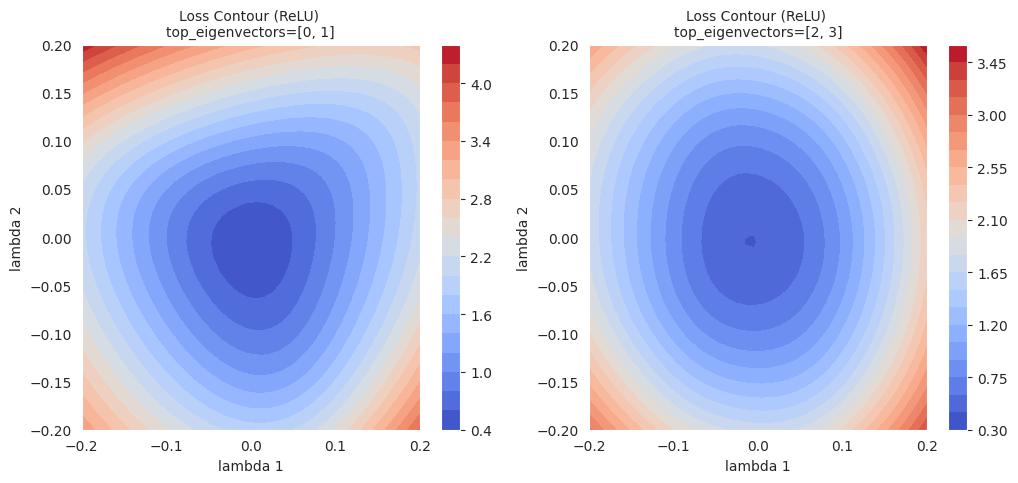
El mapa de contornos proporciona información más rica sobre el área local en comparación con la interpolación lineal simple. Mientras que la interpolación lineal muestra los cambios en los valores de la función de pérdida a lo largo de una ruta unidimensional entre dos modelos, el mapa de contornos visualiza los cambios en la función de pérdida en un plano bidimensional con ejes definidos por las dos direcciones seleccionadas (\(\lambda_1\), \(\lambda_2\)). De esta manera, se pueden identificar sutiles cambios a lo largo del camino de optimización, mínimos locales y puntos de silla en el área circundante que no se pueden detectar con interpolación lineal, así como las barreras entre ellos.

5.3.2 Técnicas avanzadas de análisis de la superficie de pérdida

Más allá de visualizaciones simples (interpolación lineal, mapas de contorno), se están investigando técnicas de análisis avanzado para comprender más profundamente la superficie de pérdida de los modelos de deep learning.

1. Análisis topológico (Topological Data Analysis, TDA):

   • Idea clave: Utiliza herramientas de topología para analizar la “forma” de la superficie de pérdida, como su conectividad.
   • Técnicas principales: Homología persistente, algoritmo Mapper, etc.
   • Aplicación: Permite comprender la complejidad de la superficie de pérdida, la estructura de conexión de los mínimos locales, las características de los puntos de silla, y obtener insights sobre la dinámica del aprendizaje y el rendimiento de la generalización. (Para más detalles, ver “Profundizando: Análisis topológico de la superficie de pérdida”)

2. Análisis multi-escala (Multi-scale Analysis):

   • Idea clave: Analiza la superficie de pérdida a diferentes escalas para comprender tanto las estructuras macroscópicas como microscópicas.
   • Técnicas principales: Transformada wavelet, teoría del espacio de escala, etc.
   • Aplicación: Permite analizar la rugosidad de la superficie de pérdida y la distribución de características a diferentes escalas, lo que ayuda a entender el funcionamiento de los algoritmos de optimización y las dificultades del aprendizaje. (Para más detalles, ver “Profundizando: Análisis multi-escala de la superficie de pérdida”)

Estas técnicas avanzadas de análisis proporcionan información más abstracta y cuantitativa sobre la superficie de pérdida, lo que contribuye a una comprensión más profunda del proceso de aprendizaje de los modelos de deep learning y al diseño de mejores estrategias de modelado y optimización.

import torch
import torch.nn as nn  # Import the nn module
from torch.utils.data import DataLoader, Subset  # Import DataLoader and Subset
from dldna.chapter_05.visualization.loss_surface import  analyze_loss_surface_multiscale
from dldna.chapter_04.utils.data import get_dataset  # Import get_dataset
from dldna.chapter_04.utils.metrics import load_model  # Import load_model

# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Load dataset and create a small subset
_, test_dataset = get_dataset(dataset="FashionMNIST")
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

# Load model (example: SimpleNetwork-ReLU)
model, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="tmp/models/")
model = model.to(device)

_ = analyze_loss_surface_multiscale(model, data_loader, loss_func, device)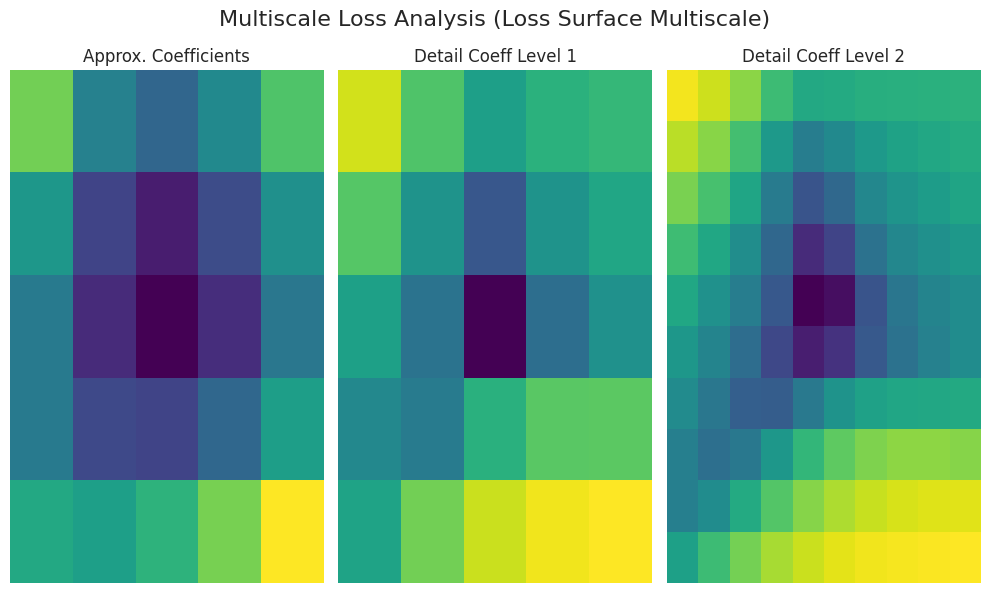

Se utilizó la función analyze_loss_surface_multiscale para analizar y visualizar la superficie de pérdida del modelo SimpleNetwork-ReLU entrenado en el conjunto de datos FashionMNIST desde una perspectiva multiscale.

Interpretación del gráfico (basada en transformada wavelet):

• Coeficientes Aproximados (coeficientes aproximados): Representan la forma general de la superficie de pérdida (estructura global). Es probable que haya un mínimo en el centro (valores de baja pérdida).

• Coef. Detalle Nivel 1/2 (coeficientes detallados): Representan cambios a una escala más pequeña. “Nivel 1” muestra la escala intermedia, mientras que “Nivel 2” muestra las irregularidades a la escala más fina (mínimos locales, puntos de silla, ruido, etc.).

• Color: Color oscuro (baja pérdida), color claro (alta pérdida)

• Los resultados pueden variar según la implementación de la función analyze_loss_surface_multiscale (función wavelet, niveles de descomposición, etc.).

• Esta visualización muestra solo parte de la superficie de pérdida; es difícil capturar completamente la complejidad del espacio de alta dimensión.

El análisis multiscale descompone la superficie de pérdida en múltiples escalas para mostrar estructuras multifacéticas que son difíciles de apreciar con una simple visualización. A gran escala, permite comprender las tendencias generales; a pequeña escala, permite observar los cambios locales, lo que ayuda a entender el comportamiento de los algoritmos de optimización, la dificultad del aprendizaje y el rendimiento de generalización.

Haga clic para ver el contenido (análisis de la superficie de pérdida basado en topología)

Análisis de superficies de pérdida basado en topología

La topología es el estudio de las propiedades geométricas que no cambian bajo transformaciones continuas. En el aprendizaje profundo, el análisis basado en topología se utiliza para examinar características topológicas como la conectividad, los agujeros y los vacíos de las superficies de pérdida, lo que proporciona insights sobre la dinámica del aprendizaje y el rendimiento de generalización.

Conceptos clave:

• Conjunto de nivel inferior (Sublevel Set): Dada una función \(f: \mathbb{R}^n \rightarrow \mathbb{R}\) y un valor crítico \(c\), se define como \(f^{-1}((-\infty, c]) = {x \in \mathbb{R}^n | f(x) \leq c}\). En el contexto de una función de pérdida, representa las regiones del espacio de parámetros donde la pérdida es menor o igual a un cierto valor.

• Homología persistente (Persistent Homology): Rastrea los cambios en los conjuntos de nivel inferior y registra la creación y anulación de características topológicas (componentes conectados, lazos, vacíos, …).

  • Características de orden 0 (Componentes Conectados): Número de regiones que están interconectadas. En las superficies de pérdida, está relacionado con el número de mínimos locales.
  • Características de orden 1 (Lazos): Número de lazos cerrados. En las superficies de pérdida, se asocia con la existencia de caminos que rodean los puntos de silla.

• Diagrama de persistencia (Persistence Diagram): Muestra los valores de pérdida en los momentos de creación y anulación de cada característica topológica en un plano de coordenadas. La coordenada \(y\) (\(\text{death} - \text{birth}\)) representa la “vida” o “persistencia” de una característica, y cuanto mayor sea el valor, más estable se considera la característica.

• Distancia embotellamiento (Bottleneck Distance): Es uno de los métodos para medir la distancia entre dos diagramas de persistencia. Encuentra el mejor emparejamiento de puntos entre los dos diagramas y calcula el valor máximo de las distancias entre los puntos emparejados.

Antecedentes matemáticos (resumidos):

• Complejo simplicial (Simplicial Complex): Concepto que generaliza puntos, líneas, triángulos, tetraedros, etc., y se utiliza para aproximar espacios topológicos.
• Operador de borde (Boundary Operator): Operador que calcula el borde de un complejo simplicial.
• Grupo de homología (Homology Group): Grupo definido usando el operador de borde, que representa los “agujeros” en un espacio topológico.
• Algoritmo de homología persistente (Persistent Homology Algorithm): Construye un complejo simplicial a través de la filtración de conjuntos de nivel inferior y rastrea los cambios en el grupo de homología para calcular el diagrama de persistencia. (Para más detalles, ver referencia [1])

Aplicación en investigación de aprendizaje profundo: * Análisis de la estructura de la superficie de pérdida: A través del diagrama de persistencia, se puede determinar la complejidad de la superficie de pérdida, el número de mínimos locales y su estabilidad, así como la existencia de puntos de silla. * Ejemplo: Gur-Ari et al., 2018 calcularon el diagrama de persistencia de la superficie de pérdida de redes neuronales y demostraron que las redes anchas (wide) tienen una estructura topológica más simple en comparación con las redes estrechas (narrow). * Predicción del rendimiento de generalización: Las características del diagrama de persistencia (por ejemplo, la duración de la característica 0 de mayor vida) pueden estar correlacionadas con el rendimiento de generalización del modelo. * Ejemplo: Perez et al., 2022 propusieron un método para predecir el rendimiento de generalización del modelo utilizando características del diagrama de persistencia. * Conectividad modal: Se buscan caminos que conecten diferentes mínimos locales y se analizan las barreras de energía a lo largo de esos caminos. * Ejemplo: Garipov et al., 2018

Referencias:

1. Edelsbrunner, H., & Harer, J. (2010). Computational Topology: An Introduction. American Mathematical Society.
2. Gur-Ari, G., Roberts, D. A., & Dyer, E. (2018). Gradient descent happens in a tiny subspace. arXiv preprint arXiv:1812.04754.
3. Perez, D., Masoomi, A., DiCecco, J., & Chwialkowski, K. (2022). Relating loss landscape topology to generalization with persistent homology. In International Conference on Machine Learning (pp. 17953-17977). PMLR.
4. Garipov, T., Izmailov, P., Podoprikhin, D., Vetrov, D. P., & Wilson, A. G. (2018). Loss surfaces, mode connectivity, and fast ensembling of dnns. Advances in neural information processing systems, 31.

Haga clic para ver el contenido (análisis profundo: análisis de superficie de pérdida multiscale)

Análisis de superficie de pérdida a múltiples escalas

La superficie de pérdida de los modelos de deep learning presenta características en diversas escalas. Desde valles y crestas grandes hasta baches y hoyos pequeños, las estructuras geométricas de diferentes tamaños influyen en el proceso de aprendizaje. El análisis a múltiples escalas es un método que separa y analiza estas características de diferentes escalas.

Idea principal:

• Transformada de ondaletas (Wavelet Transform): La transformada de ondaletas es una herramienta matemática que descompone una señal en componentes de frecuencia. Al aplicarla a la función de pérdida, se pueden separar características a diferentes escalas.

  • Transformada continua de ondaletas (Continuous Wavelet Transform, CWT):

    \(W(a, b) = \int\_{-\infty}^{\infty} f(x) \psi\_{a,b}(x) dx\)

    • \(f(x)\): función a analizar (función de pérdida)
    • \(\psi\_{a,b}(x) = \frac{1}{\sqrt{a}}\psi(\frac{x-b}{a})\): función de ondaleta (función madre de ondaleta \(\psi\) escalada (\(a\)) y trasladada (\(b\)))
    • \(W(a, b)\): coeficiente de ondaleta en la escala \(a\), posición \(b\)

  • Función madre de ondaleta: función que cumple ciertas condiciones (por ejemplo, Mexican hat wavelet, Morlet wavelet) (ver referencia [2] para más detalles)

• Análisis multiresolución (Multi-resolution Analysis, MRA): Método que descompone una señal en diferentes niveles de resolución al discretizar la CWT.

Fondo matemático (resumido):

• Función de escalamiento: función que representa los componentes de baja frecuencia.
• Función de ondaleta: función que representa los componentes de alta frecuencia.
• Descomposición: descomponer la señal en una combinación de funciones de escalamiento y ondaletas.
• Reconstrucción: reconstruir la señal original a partir de las señales descompuestas. (ver referencia [1] para más detalles)

Aplicaciones en investigación de deep learning:

• Análisis de rugosidad de la superficie de pérdida: A través de la transformada de ondaletas, se puede cuantificar la rugosidad de la superficie de pérdida y analizar su impacto en la velocidad de aprendizaje y el rendimiento de generalización.

  • Ejemplo: Li et al., 2019 usaron un análisis multiresolución basado en ondaletas para analizar el impacto de la rugosidad de la superficie de pérdida en la dinámica del aprendizaje.

• Análisis de algoritmos de optimización: Analizar cómo los algoritmos de optimización se mueven a lo largo de las características en cada escala para comprender mejor su funcionamiento.

Referencias: 1. Mallat, S. (2008). Un recorrido por las ondículas en el procesamiento de señales: el camino escaso. Academic press. 2. Daubechies, I. (1992). Diez lecciones sobre ondículas. Society for industrial and applied mathematics. 3. Li, Y., Hu, W., Zhang, Y., & Gu, Q. (2019). Análisis multirresolución del paisaje de pérdida de redes profundas. arXiv preprint arXiv:1910.00779.

5.4 Visualización del proceso de optimización: explorando los secretos del aprendizaje profundo con la función gaussiana

La superficie de pérdida real de un modelo de aprendizaje profundo existe en un espacio de ultra alta dimensión que puede tener millones o incluso billones de dimensiones, y presenta una estructura geométrica muy compleja. Por lo tanto, visualizar y analizar directamente esta superficie es prácticamente imposible. Además, la superficie de pérdida real presenta diversos problemas como puntos no diferenciables, discontinuidades e inestabilidades numéricas, lo que dificulta su análisis teórico.

5.4.1 Análisis aproximado mediante funciones gaussianas: insights ocultos en la simplicidad

Para superar estas limitaciones y entender conceptualmente el proceso de optimización, utilizamos la función gaussiana (Gaussian function), que es suave (smooth), continua (continuous) y convexa, para aproximar (approximate) la superficie de pérdida.

Razones para usar funciones gaussianas (ventajas de la aproximación de la superficie de pérdida):

1. Diferenciabilidad: La función gaussiana es infinitamente diferenciable en todos los puntos, lo cual es una condición esencial para aplicar y analizar algoritmos de optimización basados en el descenso del gradiente (gradient descent).
2. Convexidad: Una sola función gaussiana es convexa. Las funciones convexas tienen un único mínimo global, lo que facilita el análisis de la convergencia de los algoritmos de optimización.
3. Simetría: La función gaussiana tiene una forma simétrica respecto a su punto central, lo que significa que no hay sesgo en direcciones específicas de la superficie de pérdida, simplificando las suposiciones para el análisis del comportamiento del algoritmo de optimización.
4. Simplicidad matemática: La función gaussiana se puede expresar con una fórmula relativamente simple, lo que facilita su análisis matemático y permite entender teóricamente el funcionamiento de los algoritmos de optimización y derivar resultados predecibles.
5. Complejidad ajustable: Se puede ajustar la complejidad utilizando modelos mixtos gaussianos (Gaussian Mixture Models, GMM).

Fórmula de la función gaussiana:

\(z = A \exp\left(-\left(\frac{(x-x_0)^2}{2\sigma_1^2} + \frac{(y-y_0)^2}{2\sigma_2^2}\right)\right)\)

• \(A\): amplitud - altura máxima de la función de pérdida
• \(x_0\), \(y_0\): centro - posición del mínimo de la función de pérdida
• \(\sigma_1\), \(\sigma_2\): desviaciones estándar en las direcciones x e y - ancho de la superficie de pérdida (ancho o estrecho)

Por supuesto, la superficie de pérdida real puede ser mucho más compleja que una función gaussiana (con múltiples mínimos locales, puntos de silla, mesetas, etc.). Sin embargo, la aproximación mediante una sola función gaussiana proporciona un punto de partida útil para comprender las características básicas del comportamiento del algoritmo de optimización (por ejemplo, velocidad de convergencia, patrones de oscilación) y comparar diferentes algoritmos. Para simular superficies de pérdida más complejas, se pueden usar modelos mixtos gaussianos que combinan múltiples funciones gaussianas.

En esta sección, utilizaremos una sola función gaussiana para aproximar la superficie de pérdida y aplicaremos diversos algoritmos de optimización (SGD, Adam, etc.) para visualizar las trayectorias de aprendizaje, permitiéndonos comprender intuitivamente las características dinámicas y los puntos fuertes y débiles de cada algoritmo.

import torch
import numpy as np
import torch.nn as nn
from torch.utils.data import DataLoader, Subset
from dldna.chapter_05.visualization.loss_surface import hessian_eigenvectors, xy_perturb_loss, visualize_loss_surface, linear_interpolation
from dldna.chapter_04.utils.data import get_dataset  
from dldna.chapter_04.utils.metrics import load_model  
from dldna.chapter_05.optimizers.basic import SGD, Adam
from dldna.chapter_05.visualization.gaussian_loss_surface import (
    get_opt_params,  visualize_gaussian_fit, train_loss_surface, visualize_optimization_path
)


# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Get the dataset
_, test_dataset = get_dataset(dataset="FashionMNIST")
# Create a small dataset
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

trained_model, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="tmp/models/")
# trained_model, _ = load_model(model_file="SimpleNetwork-Tanh.pth", path="tmp/models/")

trained_model = trained_model.to(device)

# Loss surface data generation
top_n = 2
top_eigenvalues, top_eignevectors = hessian_eigenvectors(
    model=trained_model,
    loss_func=loss_func,
    data_loader=data_loader,
    top_n=top_n,
    is_cuda=True
)

# Define lambda range
d_min, d_max, d_num = -1, 1, 30
lambda1 = np.linspace(d_min, d_max, d_num).astype(np.float32)
lambda2 = np.linspace(d_min, d_max, d_num).astype(np.float32)

# Calculate loss surface
x, y, z = xy_perturb_loss(
    model=trained_model,
    top_eigenvectors=top_eignevectors,
    data_loader=data_loader,
    loss_func=loss_func,
    lambda1=lambda1,
    lambda2=lambda2,
    device=device
)


# After generating loss surface data
popt, _, offset = get_opt_params(x, y, z)

# Visualize Gaussian fitting
visualize_gaussian_fit(x, y, z, popt, offset, d_min, d_max, d_num)

# View from a different angle
visualize_gaussian_fit(x, y, z, popt, offset, d_min, d_max, d_num,
                      elev=30, azim=45)

Function parameters = [29.27164346 -0.0488573  -0.06687705  0.7469189   0.94904458]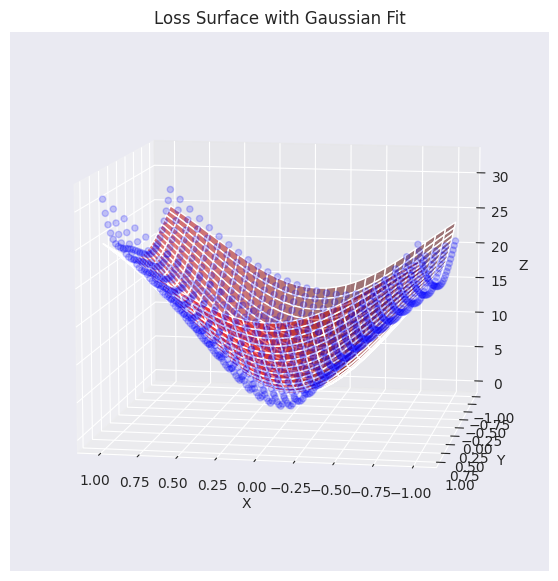

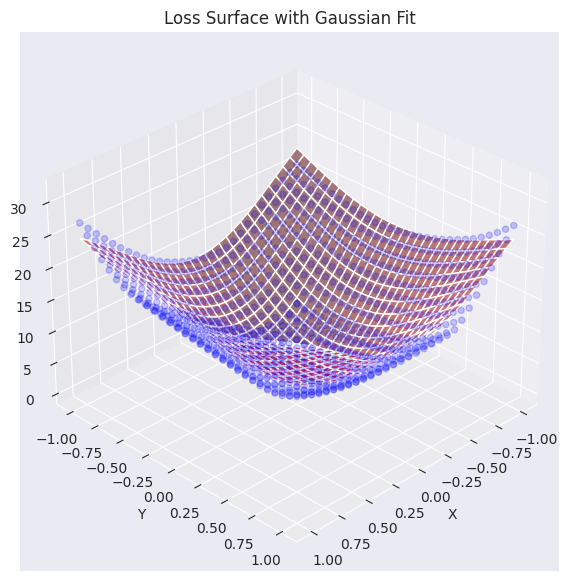
Se ha visualizado el plano de datos de pérdida real (puntos azules) superpuesto con el plano aproximado mediante una función gaussiana (rojo). Como se puede ver en el gráfico, la función gaussiana generada captura bastante bien la tendencia general de los datos de la superficie de pérdida original (especialmente, la forma cóncava del centro), generando una superficie similar. Ahora utilizaremos esta función de plano de pérdida aproximado para analizar y visualizar cómo diferentes algoritmos de optimización (optimizers) encuentran el mínimo.

5.4.2 Visualización de trayectorias

Utilizando una superficie de pérdida aproximada con una función gaussiana, visualizaremos cómo funciona el optimizador en un plano 2D.

Original text:

Traducción:

# Gaussian fitting
popt, _, offset = get_opt_params(x, y, z)
gaussian_params = (*popt, offset)

# Calculate optimization paths
points_sgd = train_loss_surface(
    lambda params: SGD(params, lr=0.1),
    [d_min, d_max], 100, gaussian_params
)
points_sgd_m = train_loss_surface(
    lambda params: SGD(params, lr=0.05, momentum=0.8),
    [d_min, d_max], 100, gaussian_params
)
points_adam = train_loss_surface(
    lambda params: Adam(params, lr=0.1),
    [d_min, d_max], 100, gaussian_params
)

# Visualization
visualize_optimization_path(
    x, y, z, popt, offset,
    [points_sgd, points_sgd_m, points_adam],
    act_name="ReLU"
)

El gráfico muestra las trayectorias de aprendizaje de tres algoritmos de optimización: SGD, Momentum SGD y Adam, en una superficie de pérdida aproximada por una función gaussiana. En áreas tanto suaves como abruptas, los tres algoritmos muestran características distintas.

• SGD (naranja): En las áreas donde la pendiente es suave, avanza hacia el mínimo con un movimiento oscilatorio relativamente amplio, pero en las áreas de pendientes pronunciadas, muestra una oscilación aún mayor, y cerca del mínimo presenta una tendencia a converger más lentamente.
• Momentum SGD (verde): Se acerca al mínimo con un menor movimiento oscilatorio y una curva más suave en comparación con el SGD. Gracias al efecto de inercia, puede encontrar el mínimo de manera más estable incluso en áreas de pendientes pronunciadas.
• Adam (rojo): Avanza hacia el mínimo con las menores oscilaciones, reaccionando sensiblemente a los cambios de pendiente y siguiendo un camino eficiente. En particular, muestra una convergencia más rápida incluso en áreas de pendientes pronunciadas. Esto se debe al mecanismo de ajuste de la tasa de aprendizaje adaptativa (adaptive learning rate) de Adam.

En la práctica, el SGD con momentum es mucho más preferido que el SGD simple, y los algoritmos de optimización adaptativos como Adam o AdamW también son ampliamente utilizados. En general, la superficie de pérdida tiende a ser plana en la mayoría de las áreas, pero cerca del mínimo presenta una forma de valle estrecho y profundo. Esto hace que una tasa de aprendizaje alta corra el riesgo de pasar por alto o diverger del mínimo, por lo que es común usar un programador de tasas de aprendizaje (learning rate scheduler) para reducir gradualmente la tasa de aprendizaje. Además, es importante considerar no solo la elección del algoritmo de optimización, sino también una tasa de aprendizaje adecuada, el tamaño del lote, las técnicas de regularización, entre otros.

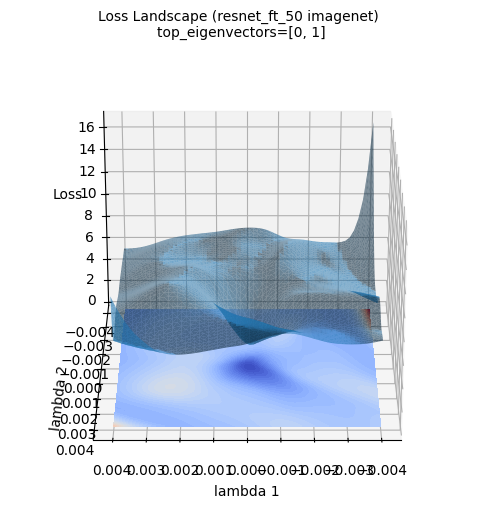
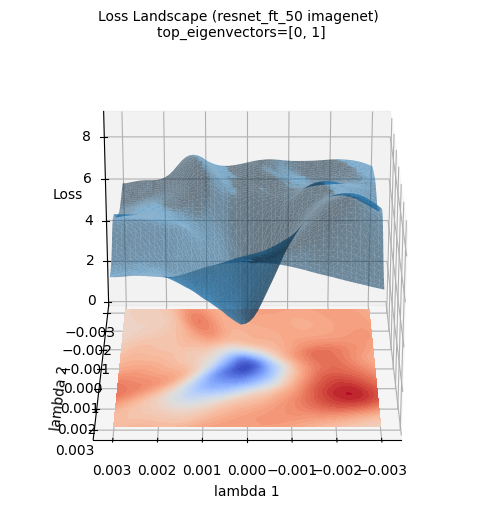
Las imágenes anteriores de la superficie de pérdida muestran una visualización tridimensional de la superficie de pérdida del modelo ResNet-50 entrenado con el conjunto de datos ImageNet. (Se usaron los dos primeros autovectores del gradiente hessiano calculado con PyHessian como ejes). A diferencia de la aproximación por función gaussiana, se puede ver que la superficie de pérdida de un modelo de aprendizaje profundo real es mucho más compleja y irregular. Sin embargo, se observa que la tendencia general de tener el mínimo en el centro (área azul) se mantiene. Estas visualizaciones ayudan a entender intuitivamente cuán complicada es la topografía de la superficie de pérdida de un modelo de aprendizaje profundo y por qué la optimización es un problema difícil.

5.5 Análisis dinámico del proceso de optimización: exploración de la trayectoria de aprendizaje

Entender las características dinámicas (dynamics) de cómo los algoritmos de optimización encuentran el mínimo de la función de pérdida en el aprendizaje de modelos de deep learning es importante. Especialmente con la aparición de modelos de lenguaje a gran escala (LLM), el análisis y control de las dinámicas de aprendizaje de modelos con miles de millones de parámetros se ha vuelto aún más crítico.

5.5.1 Características del proceso de entrenamiento

El proceso de aprendizaje de un modelo de deep learning puede dividirse en etapas inicial, media y final, cada una con sus propias características.

1. Características por etapa de aprendizaje:

   • Inicial: La norma del gradiente (gradient norm) es alta y fluctúa mucho, mientras que el valor de la función de pérdida disminuye rápidamente.
   • Media: El gradiente se estabiliza y los parámetros exploran la región óptima (optimal region).
   • Final: Los parámetros realizan ajustes finos (fine-tuning) alrededor del óptimo local (local optimum). (Es importante el early stopping)

2. Características de gradiente por capa:

   • En redes neuronales profundas, los gradientes tienden a ser más grandes cerca de la capa de entrada y más pequeños cerca de la capa de salida. (vanishing gradient problem)
   • Esto se debe al regreso hacia atrás (backpropagation) y a la aplicación de la regla de la cadena (chain rule).
   • Las conexiones residuales (residual connections) ayudan a mitigar este desequilibrio, permitiendo un aprendizaje más estable en capas profundas.

3. Dependencia entre parámetros:

   • Los parámetros de la red neuronal son interdependientes, lo que hace que el proceso de optimización sea no lineal (nonlinear).
   • Algunos parámetros pueden tener un mayor impacto en el aprendizaje, por lo que es importante mantener un equilibrio (balance) entre los parámetros.

4. Análisis del camino de optimización:

   • El camino que siguen los parámetros sobre la superficie de pérdida durante el proceso de optimización se denomina camino de optimización (optimization path).
   • Las regiones con mínimos locales en forma de valles anchos y suaves tienden a tener un mejor rendimiento de generalización (generalization performance) que los valles estrechos y puntiagudos.
   • En espacios de alta dimensión, los puntos de silla (saddle points) son muy comunes. (algoritmos como momentum y Adam están diseñados para evitarlos)
   • En áreas planas (flat) de la superficie de pérdida, los gradientes pueden ser pequeños, lo que puede hacer que el aprendizaje sea más lento. (algoritmos de tasa de aprendizaje adaptativa pueden ayudar)

5.5.2 Análisis y control de estabilidad del aprendizaje

Metodologías de análisis de estabilidad

Para analizar la estabilidad (stability) del proceso de optimización, se consideran los siguientes aspectos:

1. Detección de gradientes:

   • Identificación de fenómenos de gradiente que explotan (exploding gradient) o desaparecen (vanishing gradient).
   • Observación periódica de la norma del gradiente durante el entrenamiento.

2. Análisis basado en la Hessiana:

   • La distribución de los valores propios (eigenvalue) y el número de condición (condition number) de la matriz Hessiana indican la estabilidad del camino de optimización.
   • (Ver visualizaciones basadas en la Hessiana en la Sección 5.3)

3. Monitoreo en tiempo real:

   • Monitoreo en tiempo real de la norma del gradiente, el tamaño de las actualizaciones de parámetros, los valores de la función de pérdida y las métricas de rendimiento durante el aprendizaje.

Técnicas de estabilización (Stabilization Techniques)

• Recorte de gradientes (Gradient Clipping): Limitar el tamaño del gradiente para que no supere un umbral (threshold).

  \(g \leftarrow \text{clip}(g) = \min(\max(g, -c), c)\)

• \(g\): gradiente, \(c\): valor umbral

• Tasa de aprendizaje adaptativa (Adaptive Learning Rate): Adam, RMSProp, Lion, Sophia ajustan automáticamente la tasa de aprendizaje según las estadísticas del gradiente.

• Programador de tasa de aprendizaje (Learning Rate Scheduler): disminución gradual de la tasa de aprendizaje basada en el número de épocas o la pérdida de validación.

• Optimización de hiperparámetros (Hyperparameter Optimization): búsqueda y ajuste automático de los hiperparámetros relacionados con la optimización.

Tendencias de investigación recientes

La investigación sobre dinámica de aprendizaje en la actualidad (2024) se está desarrollando en las siguientes direcciones:

• Estabilización predictiva (Predictive Stabilization): eliminación o mitigación anticipada de factores de inestabilidad mediante el análisis de la estructura del modelo, la inicialización y las características del conjunto de datos antes del aprendizaje.
• Análisis integrado (Unified Analysis): profundización en la comprensión de los algoritmos de optimización a través del análisis conjunto de información de curvatura (hessiana) y estadísticas de gradiente.
• Control automatizado (Automated Control): ajuste automático de hiperparámetros de algoritmos de optimización utilizando técnicas como el aprendizaje por refuerzo.

Estas investigaciones están contribuyendo a hacer que el aprendizaje de modelos de deep learning sea más estable y eficiente, y a mejorar la comprensión del “caja negra”.

Ahora exploremos un ejemplo sencillo para analizar dinámicamente el proceso de optimización.

import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, Subset  # Import Subset
from dldna.chapter_05.visualization.train_dynamics import visualize_training_dynamics
from dldna.chapter_04.utils.data import get_dataset  
from dldna.chapter_04.utils.metrics import load_model  

# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# Load the FashionMNIST dataset (both training and testing)
train_dataset, test_dataset = get_dataset(dataset="FashionMNIST")
train_loader = DataLoader(train_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

# Load a pre-trained model (e.g., ReLU-based network)
trained_model, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="tmp/models/")
trained_model = trained_model.to(device)

# Choose an optimizer (e.g., Adam)
optimizer = optim.Adam(trained_model.parameters(), lr=0.001)

# Call the training dynamics visualization function (e.g., train for 10 epochs with the entire training dataset)
metrics = visualize_training_dynamics(
    trained_model, optimizer, train_loader, loss_func, num_epochs=20, device=device
)

# Print the final results for each metric
print("Final Loss:", metrics["loss"][-1])
print("Final Grad Norm:", metrics["grad_norm"][-1])
print("Final Param Change:", metrics["param_change"][-1])
print("Final Weight Norm:", metrics["weight_norm"][-1])
print("Final Loss Improvement:", metrics["loss_improvement"][-1])

El ejemplo anterior muestra varios aspectos de la dinámica del aprendizaje (learning dynamics) en la práctica. Utilizando un modelo SimpleNetwork-ReLU preentrenado en el conjunto de datos FashionMNIST, se realizó un entrenamiento adicional utilizando el algoritmo de optimización Adam y se visualizaron los siguientes cinco indicadores clave (metric) por época:

• Loss (pérdida): muestra cómo disminuye el valor de la función de pérdida durante el proceso de aprendizaje. (línea azul)
• Grad Norm (norma del gradiente): indica el tamaño del gradiente (L2 norm). (línea roja)
• Param Change (cambio de parámetros): representa el cambio en los parámetros (pesos) con respecto a la época anterior.
• Weight Norm (norma del peso): indica el tamaño de todos los parámetros del modelo (pesos). (línea morada)
• Loss Improvement (mejora de pérdida): muestra cuánto ha disminuido el valor de la función de pérdida en comparación con la época anterior. (línea amarilla)

Los gráficos muestran lo siguiente:

• Loss: el valor de pérdida, que era aproximadamente 0.51 al inicio de la primera época (época 1), disminuye constantemente a medida que avanza el entrenamiento y llega a aproximadamente 0.16 en la última época (época 20).
• Grad Norm: la norma del gradiente, que era relativamente alta al inicio de la primera época (aproximadamente 4.5), disminuye gradualmente a medida que avanza el entrenamiento y llega a alrededor de 2.0 en la última época.
• Param Change: el cambio en los parámetros es grande al inicio del entrenamiento, pero tiende a disminuir a medida que el entrenamiento progresa. Esto indica que el modelo se acerca gradualmente al punto óptimo y el cambio en los parámetros se vuelve más pequeño.
• Weight Norm: la norma del peso aumenta constantemente durante todo el proceso de aprendizaje. Esto significa que los parámetros del modelo se vuelven “más grandes” a medida que avanza el entrenamiento. (Sin embargo, esto no necesariamente implica sobreajuste (overfitting).)
• Loss Improvement: la mejora en la pérdida es grande al inicio del entrenamiento y tiende a disminuir a medida que el entrenamiento progresa.

A través de este ejemplo, podemos visualizar y comprender intuitivamente cómo el algoritmo de optimización minimiza la función de pérdida, cómo cambia el gradiente y los parámetros, entre otros aspectos de la dinámica del aprendizaje.

Conclusión

En este capítulo 5, hemos examinado a profundidad varios temas relacionados con la optimización, que son elementos clave en el proceso de aprendizaje de modelos de deep learning. Hemos explorado la importancia de los métodos de inicialización de pesos, los principios y características de diversos algoritmos de optimización (SGD, Momentum, Adam, Lion, Sophia, AdaFactor), así como la visualización de superficies de pérdida y el análisis de dinámica del aprendizaje para comprender mejor el proceso de aprendizaje de modelos de deep learning.

En el capítulo 6, profundizaremos en las técnicas clave para mejorar el rendimiento de generalización de los modelos de deep learning, como la regularización (regularization). Estudiaremos los principios y efectos de diversas técnicas de regularización, incluyendo L1/L2 regularization, dropout, batch normalization, data augmentation, y aprenderemos métodos prácticos para su aplicación a través de ejemplos.

Ejercicios de práctica

Problemas básicos

1. Cálculo manual de SGD: Calcule manualmente la regla de actualización de SGD para la función de pérdida \(L(w) = w^2\) en al menos 3 pasos, con una tasa de aprendizaje de 0.1 y un momento de 0.9. Establezca el peso inicial como \(w_0 = 2\).
2. Comparación de la velocidad de convergencia del descenso de gradiente: Aplique el descenso de gradiente a una función cuadrática simple \(f(x, y) = x^2 + 2y^2\) y compare la velocidad de convergencia cambiando la tasa de aprendizaje a 0.1, 0.01, 0.001.
3. Comparación de métodos de inicialización: Compare la inicialización Kaiming con la inicialización Xavier y explique por qué la inicialización Kaiming es más adecuada cuando se usa con la función de activación ReLU.

Problemas aplicados

1. Optimizador Adam: Explique el principio de funcionamiento del optimizador Adam (incluyendo las fórmulas) y describa los roles de los parámetros \(\beta_1\) y \(\beta_2\).
2. Normalización por lotes y inicialización: Explique cómo la normalización por lotes (Batch Normalization) reduce la importancia del método de inicialización y proporcione razones para ello.
3. Plano de pérdida gaussiano: En el ejemplo de aproximación del plano de pérdida usando una función gaussiana (sección 5.5.1), explique cómo los parámetros de la función gaussiana (amplitud, punto central, varianza) afectan el proceso de optimización. (Observe cómo cambia la trayectoria de optimización al modificar cada parámetro).

Problemas avanzados

1. Análisis del optimizador Lion: Explique la idea principal del optimizador Lion (incluyendo las fórmulas) y analice sus ventajas y desventajas en comparación con Adam.
2. Experimento de métodos de inicialización: Aplique diferentes métodos de inicialización (LeCun, Xavier, Kaiming, Ortogonal) a un conjunto de datos dado (por ejemplo, FashionMNIST) y un modelo (SimpleNetwork del capítulo 5.1), y compare los resultados (tasas de error, velocidad de convergencia, número condicionado promedio, norma espectral, relación de rango efectivo).
3. Visualización de trayectorias de optimización: Utilizando el código de visualización de trayectorias de optimización del capítulo 5.5, defina su propia función de pérdida (por ejemplo, una función multimodal o no convexa) y visualice y compare las trayectorias de optimización de varios optimizadores (SGD, Momentum, Adam, Lion, etc.). (Compare al menos 3 optimizadores diferentes).

Haga clic para ver el contenido (análisis de la superficie de pérdida basado en topología)

Soluciones de ejercicios

Problemas básicos

1. Cálculo manual de SGD:

   • Paso 1:
     • \(g_0 = \frac{dL}{dw}(w_0) = 2w_0 = 4\)
     • \(v_0 = 0\) (valor inicial del momento)
     • \(w_1 = w_0 - \eta v_1 = 2 - 0.1 \cdot (0.9 \cdot 0 + 4) = 1.6\)
   • Paso 2:
     • \(g_1 = 2w_1 = 3.2\)
     • \(v_1 = 0.9 \cdot v_0 + g_0= 0.9 \cdot 0 + 4 = 4\)
     • \(w_2 = w_1 - \eta \cdot (0.9 \cdot v_1 + g_1) = 1.6 - 0.1 \cdot (0.9 \cdot 4+ 3.2) = 0.92\)
   • Paso 3:
     • \(g_2 = 2w_2 = 1.84\)
     • \(v_2 = 0.9 \cdot 4 + 3.2 = 6.8\)
     • \(w_3 = w_2 - \eta \cdot (0.9 * v_2 + g_2) = 0.92 - 0.1 \cdot (0.9 \cdot 6.8 + 1.84) = 0.124\)

2. Comparación de la velocidad de convergencia del descenso por gradiente:

   • Cuanto mayor es la tasa de aprendizaje (0.1), más rápida es la convergencia inicial, pero puede producirse vibración cerca del punto óptimo.
   • Cuanto menor es la tasa de aprendizaje (0.001), más lenta es la velocidad de convergencia, pero se acerca al punto óptimo de manera más estable.
   • Una tasa de aprendizaje adecuada (0.01) muestra una velocidad de convergencia y estabilidad moderadas.

3. Comparación de métodos de inicialización:

   • Inicialización Kaiming: Considera la característica de la función de activación ReLU (convierte entradas negativas en 0), y inicializa los pesos con una distribución que tiene una desviación estándar de \(\sqrt{2/n_{in}}\).
   • Inicialización Xavier: Independientemente del tipo de función de activación, utiliza una desviación estándar de \(\sqrt{2/(n_{in} + n_{out})}\) para mantener la varianza de las entradas y salidas.
   • ReLU + Kaiming: Utiliza una distribución con una desviación estándar de \(\sqrt{2/n_{in}}\) para proporcionar una inicialización adecuada que funcione bien con ReLU, evitando el problema de los gradientes que se apagan.

Problemas avanzados

1. Normalización por lotes y métodos de inicialización:

   • La normalización por lotes ayuda a estabilizar el entrenamiento al reducir la covarianza cambiante interna.
   • Se puede combinar con métodos de inicialización como Kaiming o Xavier para mejorar aún más el rendimiento del modelo.

2. Normalización por lotes y aprendizaje:

   • La normalización por lotes puede acelerar la convergencia del entrenamiento y permitir una tasa de aprendizaje más alta.
   • También ayuda a reducir la dependencia entre las capas, lo que facilita el entrenamiento de redes más profundas.

• Normalización por lotes: normaliza las entradas de cada mini-lote a una media de 0 y una varianza de 1.
  • Reducción de la importancia de la inicialización: la normalización por lotes reduce el cambio de covarianza interna (internal covariate shift) en la red, disminuyendo así la dependencia de la distribución de los pesos iniciales.
  • Razón: las entradas normalizadas sitúan las funciones de activación dentro de un rango adecuado (por ejemplo, el rango positivo de ReLU), lo que alivia los problemas de desvanecimiento y explosión del gradiente y estabiliza el aprendizaje.

3. Plano de pérdida gaussiano:
   • Amplitud (A): ajusta la magnitud general de la función de pérdida. Si la amplitud es grande, el rango de cambio de los valores de pérdida puede ser mayor, lo que podría hacer que el aprendizaje sea inestable.
   • Punto central (\(x_0\), \(y_0\)): determina la ubicación del mínimo de la función de pérdida. El algoritmo de optimización se moverá hacia este punto central.
   • Varianza (\(\sigma_1\), \(\sigma_2\)): indica el grado de cambio de la función de pérdida en cada dirección del eje. Una varianza pequeña resulta en una forma estrecha y afilada, mientras que una grande produce una forma ancha y suave. Si las varianzas son diferentes, se deben ajustar los tasas de aprendizaje en cada dirección de manera diferente.

Problemas avanzados

1. Análisis del optimizador Lion:

   • Idea clave: realiza actualizaciones utilizando solo el signo (sign) del gradiente.
   • Fórmula: c_t = β_1 * m_{t-1} + (1 - β_1) * g_t w_{t+1} = w_t - η * sign(c_t) m_t = c_t
     • solo se utiliza el signo de la actualización, por lo que no es necesario calcular ni almacenar el segundo momento como en Adam.
   • Ventajas:
     • consume menos memoria que Adam (no almacena el segundo momento).
     • el tamaño de las actualizaciones es uniforme para todos los parámetros, lo que lo hace robusto a gradientes escasos.
   • Desventajas:
     • ignora la magnitud del gradiente, lo que puede resultar en una convergencia más lenta que Adam en ciertas situaciones.
     • el ajuste de la tasa de aprendizaje puede ser más sensible que en Adam.

2. Experimentación con métodos de inicialización:

   • Diseño del experimento:
     • se utiliza el mismo modelo (SimpleNetwork) y conjunto de datos (FashionMNIST).
     • se aplican los métodos de inicialización LeCun, Xavier, Kaiming y Ortogonal.
     • se usa el mismo algoritmo de optimización (por ejemplo, Adam) y tasa de aprendizaje.
     • se entrena durante un número suficiente de épocas (por ejemplo, 20), registrando las métricas de evaluación (tasa de error, velocidad de convergencia, condición media, norma espectral, relación de rango efectivo) en cada época.
   • Análisis de resultados:
     • si se usa la función de activación ReLU, Kaiming inicialización probablemente tenga el mejor rendimiento.
     • la inicialización Ortogonal puede dar buenos resultados en RNN/LSTM.
     • Xavier inicialización puede ser buena para funciones de activación tanh y sigmoid.
     • LeCun inicialización puede tener un rendimiento inferior en redes modernas.

3. Visualización del camino de optimización:

• Definir su propia función de pérdida:
• Ejemplo: \(f(x, y) = (x^2 + y - 11)^2 + (x + y^2 - 7)^2\) (Función de Himmelblau, función multimodal)
• Ejemplo: \(f(x, y) = 0.5x^2 - 0.25y^2 + 3\) (Función no convexa con puntos de silla)
• Seleccionar algoritmo de optimización: SGD, Momentum(SGD with momentum), Adam, Lion
• Visualización: Consulte el código del Capítulo 5.5 para visualizar la trayectoria de optimización de cada optimizador en un plano bidimensional.
• Análisis de resultados:
  • SGD tiene una alta probabilidad de quedar atrapado en mínimos locales/puntos de silla.
  • Momentum puede escapar de mínimos locales gracias a su inercia, pero puede oscilar.
  • Adam puede alcanzar el óptimo más eficientemente gracias a su tasa de aprendizaje adaptativa.
  • Lion puede mostrar un comportamiento similar o incluso una convergencia más rápida que Adam, pero puede ser sensible al ajuste de la tasa de aprendizaje.
  • Analice y compare los resultados de optimización según la forma de la función de pérdida, como múltiples picos y puntos de silla.

Referencia

1. An overview of gradient descent optimization algorithms (Sebastian Ruder, 2016) - Un excelente resumen de los algoritmos de optimización en el aprendizaje profundo. Compara y analiza varios algoritmos como SGD, Momentum, AdaGrad, RMSProp, Adam, entre otros.
2. Visualizing the Loss Landscape of Neural Nets (Li et al., 2018) - Un artículo pionero sobre la visualización de las superficies de pérdida. Muestra cómo las conexiones residuales (residual connections) aplanan la superficie de pérdida.
3. Optimization for Deep Learning Highlights in 2023 (Sebastian Ruder, 2023) - Un artículo de blog que resume los puntos clave de la optimización en el aprendizaje profundo para 2023. Es útil para estar al tanto de las últimas tendencias en investigación.
4. Improving Deep Learning with Better Initialization (Mishkin & Matas, 2021) - Un artículo que presenta la última investigación sobre métodos de inicialización modernos. Compara diferentes técnicas de inicialización y proporciona directrices prácticas.
5. Symbolic Discovery of Optimization Algorithms (Chen et al., 2023) - Un artículo sobre el algoritmo Lion descubierto por Google Brain.
6. PyHessian: Neural Networks Through the Lens of the Hessian (Yao et al., 2020) - Un artículo sobre la herramienta PyHessian, que utiliza la matriz Hessiana para analizar las superficies de pérdida.
7. The Marginal Value of Adaptive Gradient Methods in Machine Learning (Wilson et al., 2017) - Un artículo que cuestiona el valor marginal de los métodos de gradiente adaptativo en el aprendizaje automático.
8. A Closer Look at Smoothness in Deep Learning: A Tensor Decomposition Approach (Li et al., 2024) - Un artículo que utiliza la descomposición de tensores para analizar la suavidad en los modelos de aprendizaje profundo.
9. Understanding Measures of Efficiency for Stochastic Optimization (Defazio & Bottou, 2025) - Un artículo que propone métodos para medir la eficiencia de los algoritmos de optimización estocástica.
10. Deep Learning (Goodfellow, Bengio, Courville, 2016) - Un libro de texto sobre aprendizaje profundo. Los capítulos 6 (Redes Neuronales Feedforward Profundas) y 8 (Optimización para el Entrenamiento de Modelos Profundos) tratan temas relacionados con la inicialización y la optimización.
11. Stanford CS231n: Convolutional Neural Networks for Visual Recognition - Un curso de Stanford sobre redes neuronales convolucionales. La sección de optimización cubre temas relacionados con la optimización.
12. Papers with Code - Optimization Methods - Un sitio web que recopila los últimos artículos sobre métodos de optimización.
13. An overview of gradient descent optimization algorithms (Sebastian Ruder, 2016) - Un excelente resumen de los algoritmos de optimización de descenso de gradiente en aprendizaje profundo. Compara y analiza diversos algoritmos como SGD, Momentum, AdaGrad, RMSProp, Adam, entre otros.
14. Visualizing the Loss Landscape of Neural Nets (Li et al., 2018) - Un trabajo pionero en la visualización del paisaje de pérdida de redes neuronales. Muestra cómo las conexiones residuales (residual connection) aplanan el paisaje de pérdida.
15. Optimization for Deep Learning Highlights in 2023 (Sebastian Ruder, 2023) - Un blog que resume los puntos clave de la optimización en aprendizaje profundo para 2023. Es útil para estar al día con las tendencias de investigación más recientes.
16. Improving Deep Learning with Better Initialization (Mishkin & Matas, 2021) - Un estudio que aborda las tendencias modernas en la inicialización de redes neuronales. Compara varios métodos de inicialización y proporciona directrices prácticas.
17. Symbolic Discovery of Optimization Algorithms (Chen et al. 2023) - Un artículo sobre el descubrimiento del algoritmo Lion por parte de Google Brain.
18. PyHessian: Neural Networks Through the Lens of the Hessian (Yao et al., 2020) - Un artículo sobre PyHessian, una herramienta para analizar el paisaje de pérdida utilizando la matriz Hessiana.
19. The Marginal Value of Adaptive Gradient Methods in Machine Learning (Wilson et al., 2017) - Un estudio que demuestra que los métodos de gradiente adaptativo (como Adam) no siempre son mejores que SGD.
20. How to escape saddle points efficiently (Ge et al., 2015) - Un artículo de blog que explica cómo usar el descenso de gradiente perturbado (perturbed gradient descent) para escapar eficientemente de los puntos de silla.
21. Deep Understanding of Modern Initialization Methods with Block Diagonal Matrices (Huang et al., 2021) - Un artículo que analiza los métodos de inicialización utilizando matrices diagonales por bloques. AdaHessian: An Adaptive Second Order Optimizer for Machine Learning (Yao et al., 2020) - Artículo sobre el optimizador AdaHessian que utiliza los componentes diagonales de la matriz hessiana para aprovechar información de segundo orden. 11. A Closer Look at Smoothness in Deep Learning: A Tensor Decomposition Approach (Li et al., 2024) - Artículo que analiza la suavidad (smoothness) de los modelos de aprendizaje profundo utilizando descomposición de tensores. 12. Understanding Measures of Efficiency for Stochastic Optimization (Defazio & Bottou, 2025) - Artículo que propone métodos para medir la eficiencia de los algoritmos de optimización estocástica. 13. Deep Learning (Goodfellow, Bengio, Courville, 2016) - Libro de texto sobre aprendizaje profundo. Los capítulos 6 (Redes Neuronales Feedforward Profundas) y 8 (Optimización para el Entrenamiento de Modelos Profundos) tratan temas relacionados con la inicialización y la optimización. 14. Stanford CS231n: Convolutional Neural Networks for Visual Recognition - Curso de aprendizaje profundo de la Universidad de Stanford. La parte de optimización cubre contenido relacionado con la optimización. 15. Papers with Code - Optimization Methods - Sitio web que recopila los últimos artículos relacionados con la optimización.